Read and download free pdf of Case Study Chapter 3 Linear Equations Mathematics. Students and teachers of Class 10 Mathematics can get free printable Worksheets for Class 10 Mathematics Linear Equations in PDF format prepared as per the latest syllabus and examination pattern in your schools. Class 10 students should practice questions and answers given here for Mathematics in Class 10 which will help them to improve your knowledge of all important chapters and its topics. Students should also download free pdf of Class 10 Mathematics Worksheets prepared by teachers as per the latest Mathematics books and syllabus issued this academic year and solve important problems with solutions on daily basis to get more score in school exams and tests
Worksheet for Class 10 Mathematics Linear Equations
Class 10 Mathematics students should download to the following Linear Equations Class 10 worksheet in PDF. This test paper with questions and answers for Class 10 will be very useful for exams and help you to score good marks
Class 10 Mathematics Worksheet for Linear Equations
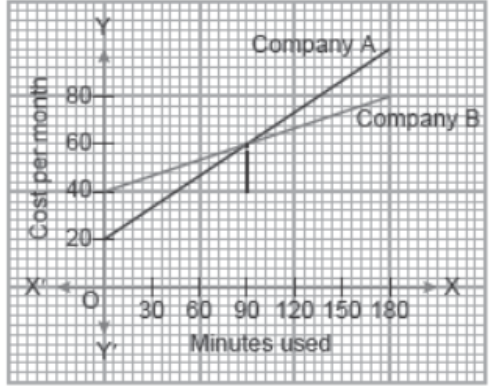
l. Read the following and answer A man is trying to choose between two phone plans. The first plan of company A, cost ` 20 per month, with calls costing an additional 25 paise per minute. The second plan of company B charges ` 40 per month, but calls cost 8 paise per minute. These two situations are shown below which represent linear equations. The total cost for the two company’s are given by
y = 0.25x + 20
and y = 0.08x + 40
where x is the minutes used and y is the total cost per month.
Question. Given system of linear equations x + 2y – 4 = 0, 2x + 4y – 12 = 0 represents
(a) parallel lines
(b) intersecting lines
(c) coincident lines
(d) can’t say
Answer: A
Question. Solution of system of linear equations x + 2y = – 1 and 2x – 3y = 12 is
(a) (–3, 2)
(b) (–3, –2)
(c) (3, – 2)
(d) (3, 2)
Answer: C
Question. If the system of pair of linear equations kx + 2y = 5, 3x + y = 1 has a unique solution, then
(a) k 2 3 !
(b) k = 6
(c) k ≠ 6
(d) k 3 2
Answer: C
Question. If a person takes first plan and calls for 90 minutes in a month then how much amount he will have to pay whose cost for a month is given by y = 0.25x + 20?
(a) ₹ 20
(b) ₹ 40
(c) ₹ 42.50
(d) ₹ 45
Answer: C
Question. Another person takes second plan and also calls for 90 minutes in a month, then the amount which he has to pay when total cost is given by y = 0.08x + 40, is
(a) ₹ 45
(b) ₹ 47
(c) ₹ 45.20
(d) ₹ 47.20
Answer: D
ll. Read the following and answer A cricket bat manufacturer’s revenue is the function used to calculate the amount of money that comes into the business. It can be represented by the equation R = xp, where x = quantity and p = price.
The revenue function is shown in orange colour in the figure. The cost function is the function used to calculate the costs of doing business. It includes fixed costs, such as rent and salaries, and variable costs such as utilities. The cost function is shown in blue colour in figure.
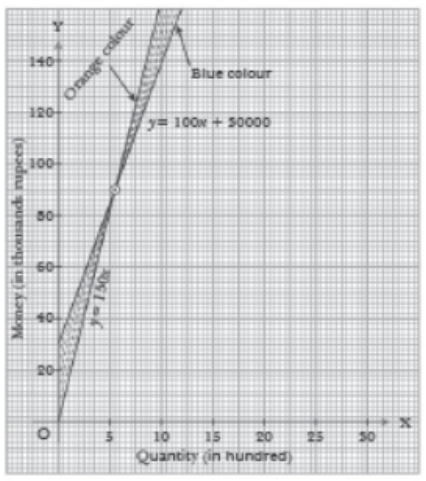
The x-axis represents quantity (in hundreds) of units, and the y-axis represents either cost or revenue (in thousand of rupees).
The profit function is the difference of revenue function and the cost function, written as
P(x) = R(x) – C(x)
Now, let C(x) = 100x + 30000 and R(x) = 150x
If we replace function by y, we get
Linear equations are y = 100x + 30000 and y = 150x
Question. The number of bat manufactured (x) so that there is no profit or loss for the manufacturer is
(a) x = 200
(b) x = 300
(c) x = 400
(d) x = 600
Answer: D
Question. Solution of the system of linear equations x + y = 1, 2x – 3y = 7, is
(a) (1, 2)
(b) (2, 1)
(c) (2, –1)
(d) (–2, –1)
Answer: C
Question. The value of k for which the system of linear equations 4x + 5y = 3 and kx + 15y = 9 has infinitely many solutions is
(a) k = 3
(b) k = 4
(c) k = 12
(d) k = 8
Answer: C
Question. If the cost and revenue are given by the linear equations y = 0.85x + 35000 and y = 1.55x respectively, and the break-even point is the point at which the two lines intersect, then its break even point is
(a) (50000, 77500)
(b) (50000, 60000)
(c) (45000, 50000)
(d) (45000, 60000)
Answer: A
Question. The system of linear equations 3x + 2y = 12, 5x – 2y = 4 represents
(a) parallel lines
(b) intersecting lines
(c) coincident lines
(d) can’t say
Answer: B
lll. Read the following and answer The scissors which is so common in our daily life use, its blades represent the graph of linear equations.
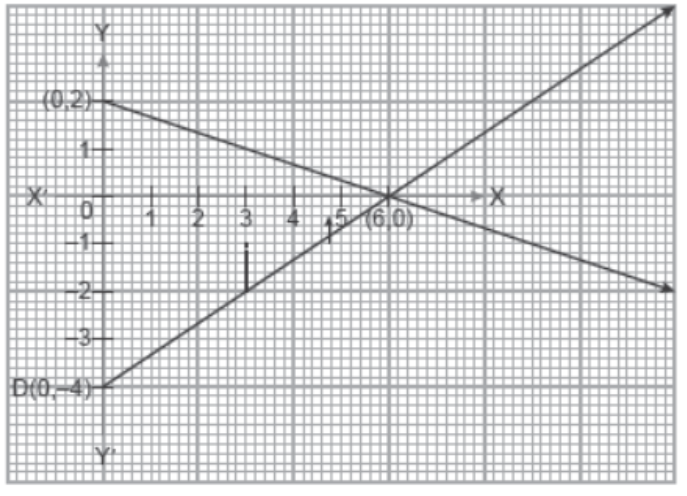
Let the blades of a scissor are represented by the system of linear equations:
x + 3y = 6 and 2x – 3y = 12
Question. If a pair of linear equations in two variables is consistent, then the lines represented by two equations are
(a) intersecting
(b) parallel
(c) always coincident
(d) intersecting or coincident
Answer: D
Question. The number of solution of the system of linear equations x + 2y – 8 = 0 and 2x + 4y = 16 is
(a) 0
(b) 1
(c) 2
(d) infinitely many
Answer: D
Question. If (1, 2) is the solution of linear equations ax + y = 3 and 2x + by = 12, then values of a and b are respectively
(a) 1, 5
(b) 2, 3
(c) –1, 5
(d) 3, 5
Answer: A
Question. The pivot point (point of intersection) of the blades represented by the linear equation x + 3y = 6 and 2x – 3y = 12 of the scissor is
(a) (2, 3)
(b) (6, 0)
(c) (3, 2)
(d) (2, 6)
Answer: B
Question. The points at which linear equations x + 3y = 6 and 2x – 3y = 12 intersect y – axis respectively are
(a) (0, 2) and (0, 6)
(b) (0, 2) and (6, 0)
(c) (0, 2) and (0, –4)
(d) (2, 0) and (0, –4)
Answer: C
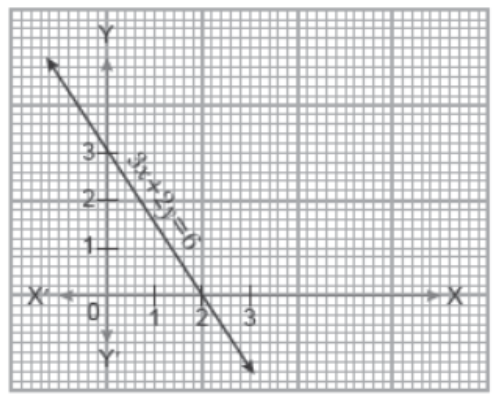
lV. Read the following and answer A pen stand with a pen is represented by the system of linear equations y = 0 and 3x + 2y = 6.
Question. The value of k for which the system of equations kx – 5y = 2 and 6x + 2y = 7 has no solution, is
(a) 30
(b) –30
(c) 15
(d) –15
Answer: D
Question. The linear equation 3x + 2y = 6 intersects the y–axis at the point
(a) (0, 3)
(b) (0, 2)
(c) (0, –3)
(d) (2, 3)
Answer: A
Question. The system of linear equations y = 0 and 3x + 2y = 6 represents the pen stand and a pen respectively then their point of contact (intersection) is
(a) (0, 3)
(b) (2, 0)
(c) (3, 2)
(d) (3, 0)
Answer: B
Question. The pair of linear equation y = x and x + y = 6 intersect each other at point
(a) (4, 2)
(b) (4, 4)
(c) (3, 3)
(d) (3, 2)
Answer: C
Question. The system of linear equations 3x + 6y = 3900 and x + 3y = 1300 represent the lines which are
(a) parallel
(b) intersecting
(c) coincident
(d) can’t say
Answer: B
V. Read the following and answer A boy enjoying the pizza with his friends and share with them by slicing it. During slicing the pizza, he noticed that the pair of linear equations formed.
Let these pair of linear equations be y – 2x = 1 and 5y – x = 14.
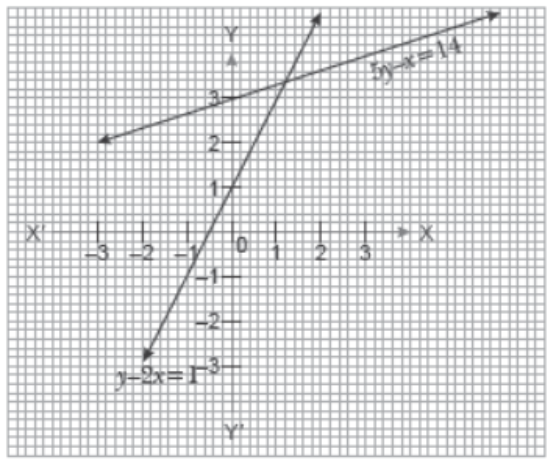
Question. The system of linear equations 2x – 3y + 6 = 0 and 2x + 3y – 18 = 0
(a) has a unique solution
(b) has no solution
(c) has infinitely many solution
(d) may or may not have a solution
Answer: A
Question. If a pair of linear equations in two variables is inconsistent, then the lines represented by two equations are
(a) intersecting
(b) parallel
(c) always coincident
(d) Intersecting or coincident
Answer: B
Question. The point of intersection of the lines given by the equations y – 2x = 1 and 5y – x = 14 is
(a) (–2, 3)
(b) (–4, 2)
(c) (6, 4)
(d) (1, 3)
Answer: D
Question. The value(s) of k for which the system of linear equations 2x – ky + 3 = 0 and 3x + 2y – 1 = 0 has no solution, is
(a) 4/3
(b) –4/3
(c) 6
(d) –6
Answer: B
Question. The linear equation y – 2x = 1 intersect the y–axis at point
(a) (−1/2 , 0)
(b) (0, 1)
(c) (0, –14)
(d) (0 , 14/5)
Answer: B
| CBSE Class 10 Mathematics Introduction to Trigonometry Worksheet Set A |
| CBSE Class 10 Mathematics Introduction to Trigonometry Worksheet Set B |
| CBSE Class 10 Mathematics Probability Worksheet Set A |
| CBSE Class 10 Mathematics Probability Worksheet Set B |
| CBSE Class 10 Mathematics Probability Worksheet Set C |
Important Practice Resources for Class 10 Mathematics
Worksheet for CBSE Mathematics Class 10 Linear Equations
We hope students liked the above worksheet for Linear Equations designed as per the latest syllabus for Class 10 Mathematics released by CBSE. Students of Class 10 should download in Pdf format and practice the questions and solutions given in the above worksheet for Class 10 Mathematics on a daily basis. All the latest worksheets with answers have been developed for Mathematics by referring to the most important and regularly asked topics that the students should learn and practice to get better scores in their class tests and examinations. Expert teachers of studiestoday have referred to the NCERT book for Class 10 Mathematics to develop the Mathematics Class 10 worksheet. After solving the questions given in the worksheet which have been developed as per the latest course books also refer to the NCERT solutions for Class 10 Mathematics designed by our teachers. We have also provided a lot of MCQ questions for Class 10 Mathematics in the worksheet so that you can solve questions relating to all topics given in each chapter.
You can download the CBSE Printable worksheets for Class 10 Mathematics Linear Equations for latest session from StudiesToday.com
There is no charge for the Printable worksheets for Class 10 CBSE Mathematics Linear Equations you can download everything free
Yes, studiestoday.com provides all latest NCERT Linear Equations Class 10 Mathematics test sheets with answers based on the latest books for the current academic session
CBSE Class 10 Mathematics Linear Equations worksheets cover all topics as per the latest syllabus for current academic year.
Regular practice with Class 10 Mathematics worksheets can help you understand all concepts better, you can identify weak areas, and improve your speed and accuracy.

