Read and download the CBSE Class 9 Mathematics Constructions Worksheet Set B in PDF format. We have provided exhaustive and printable Class 9 Mathematics worksheets for Chapter 11 Constructions, designed by expert teachers. These resources align with the 2025-26 syllabus and examination patterns issued by NCERT, CBSE, and KVS, helping students master all important chapter topics.
Chapter-wise Worksheet for Class 9 Mathematics Chapter 11 Constructions
Students of Class 9 should use this Mathematics practice paper to check their understanding of Chapter 11 Constructions as it includes essential problems and detailed solutions. Regular self-testing with these will help you achieve higher marks in your school tests and final examinations.
Class 9 Mathematics Chapter 11 Constructions Worksheet with Answers
Very Short Answer Type Questions:
Question: Can a ΔXYZ be constructed, in which XY = 5 cm, ∠X = 50° and YZ + XZ = 5 cm?
Answer: No, ΔXYZ can’t be constructed.
Since, sum of two sides of triangle must be greater than third side, but here, XY = YZ + XZ.
Question: If we bisect a line segment AB, then each of the equal part we get measures 3.8 cm. Find the length of AB.
Answer: If we bisect line segment AB, then we get each part equal to 3.8 cm.
∴ Length of AB = 2 × 3.8 cm = 7.6 cm
Question: If we draw a perpendicular bisector of a line segment AB = 9 cm which bisects AB at M, then find AM and BM.
Answer: 1. Since, perpendicular bisector of a line segment divides it into two equal parts.
∴ AM = BM = 9/2 cm = 4.5 cm
Question: Draw a straight angle. Using compass bisect it. Name the angles obtained.
Answer:
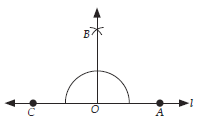
Steps of construction :
Step I : Draw any straight angle (say ∠AOC)
Step II : Draw OB , the bisector of ∠AOC.
Then, ∠AOB and ∠BOC are the required angles obtained by bisecting straight ∠AOC.
Short Answer Type Questions:
Question: Construct ΔABC such that AB = 5.8 cm, BC + CA = 7 cm and ∠B = 60°.
Answer: Steps of Construction :
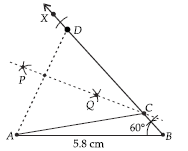
Step I : Draw a line segment AB = 5.8 cm and ∠ABX = 60°.
Step II : Cut line segment BD = 7 cm along BX .
Step III : Join AD and draw PQ, perpendicular bisector of AD.
Step IV : Let PQ intersects BD at C.
Step V : Join AC.
Hence, ΔABC is the required triangle.
Question: Draw a line segment AB = 13.2 cm. Divide it into 4 equal parts using ruler and compass. Also, measure the length of each part.
Answer: Steps of construction :
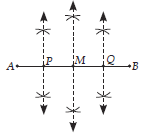
Step I : Draw a line segment AB = 13.2 cm.
Step II : Draw a perpendicular bisector of AB, which intersect AB at M.
Step III : Again, draw a perpendicular bisector of AM; which intersects AM at P.
Step IV : Also, draw a perpendicular bisector of BM, which intersects BM at Q.
Thus, AB is divided into four equal parts, where
AP = PM = MQ = QB
= 1/4 AB = 13.2/4 = 3.3 cm
Question: Draw a line segment of length 6 cm. Draw perpendicular bisector of this line segment.
Answer: Steps of construction :
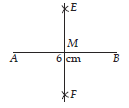
Step I : Draw a line segment AB = 6 cm by using a ruler.
Step II : With A as centre and radius more than half of AB, draw arcs on both sides of AB.
Step III : With B as centre and the same radius (as taken in previous step), draw arcs cutting the
previous arcs drawn in Step II at E and F respectively.
Step IV : Join EF intersecting AB at M.
Thus, EF is perpendicular bisector of the line segment AB.
Question: Draw line segment AB = 8.8 cm and draw its perpendicular bisector and measure the length of each part.
Answer: Steps of construction :
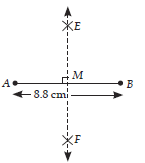
Step I : Draw a line segment AB = 8.8 cm by using graduated ruler.
Step II : Taking A as centre and radius equal to more than half of AB, draw arcs on both sides of line segment AB.
Step III : Taking B as centre and same radius as in Step II, draw arcs on both sides of AB cutting the previous arcs at E and F.
Step IV : Join EF intersecting AB at M. Then, EF is the required perpendicular bisector of AB. On measuring by graduated ruler, we find that
AM = MB = 4.4 cm.
Question: Construct ΔABC such that BC = 6 cm, ∠B = 45° and AB – AC = 3 cm.
Answer: Steps of Construction :
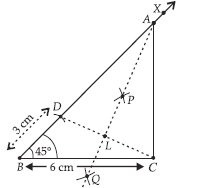
Step I : Draw BC = 6 cm and ∠CBX = 45°.
Step II : On BX, cut BD = 3 cm.
Step III : Join CD.
Step IV : Draw PQ, perpendicular bisector of CD.
Step V : PQ intersects BX at A and CD at L.
Step VI : Join AC.
Hence, ΔABC is the required triangle.
Question: Using ruler and compass only, draw an angle of measure 135°.
Answer: Steps of construction :
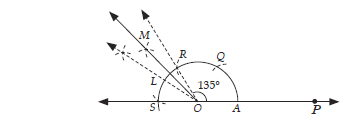
Step I : Draw a ray OP.
Step II : With centre O and a suitable radius, draw an arc which cuts OP at A.
Step III : With the same radius and starting from A, mark points Q, R and S on the arc drawn in Step II such that AQ = QR = RS
Step IV : Draw OL, the bisector of ROS.
Step V : Draw OM , the bisector of ROL.
Thus, ∠POM = ∠POR + ∠ROM = 120° + 15° = 135°
Question: Construct an equilateral triangle, the sum of its two sides is 8 cm.
Answer: We know that, in equilateral triangle, all the angles are of equal measure and all sides are of equal length.
Since, sum of two-sides of triangle is 8 cm, therefore each side of equilateral triangle will be 4 cm.
Steps of construction :
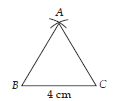
Step I : Draw the line segment BC = 4 cm.
Step II : Taking B as centre and radius
= 4 cm draw an arc.
Step III : Taking C as centre and same radius as in Step II, draw an arc cutting the previous arc at A.
Step IV : Join AB and AC.
Then, ABC is the required equilateral triangle.
Question: Construct a square of side 3 cm.
Answer: Steps of construction :
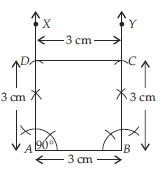
Step I : Draw a line segment AB = 3 cm.
Step II : Draw angle of 90° at points A and B of the line segment AB. Also draw AX parallel to BY.
Step III : Cut AD and BC of length 3 cm on AX and BY respectively.
Step IV : Join CD.
Then, ABCD is the required square of side 3 cm.
Question: Using ruler and compass only, draw a right angle.
Answer: Steps of construction :
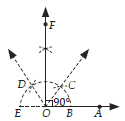
Step I : Draw a ray OA .
Step II : Taking O as centre and suitable radius, draw a semicircle, which cuts OA at B.
Step III : With B as centre and the same radius, as in Step II, draw an arc cutting the semicircle at C. Again, with C ascentre, draw an arc cutting the semicircle at D.
Step IV : Draw OC and OD .
Step V : Draw OF , the bisector of ∠COD.
Thus, ∠AOF = 90°
Long Answer Type Questions:
Question: Construct a ΔABC in which BC = 5.6 cm, AC – AB = 1.6 cm and ∠B = 45°. Justify your construction.
Answer: Steps of construction :
Step I : Draw BC = 5.6 cm.
Step II : At B, construct ∠CBX = 45°.
Step III : Produce XB to X′ to form line XBX.
Step IV : Along ray BX′, cut-off a line segment BD = 1.6 cm.
Step V : Join CD.
Step VI : Draw perpendicular bisector of CD which cuts BX at A.
Step VII : Join CA to obtain required triangle BAC.
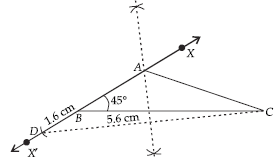
Justification:
Since A lies on the perpendicular bisector of CD.
∴ AC = AD = AB + DB = AB + 1.6 ⇒ AC – AB = 1.6 cm which justified the construction.
Question: Give reason:
(i) Construction of an angle of 22.5° is possible with the help of ruler and compass.
(ii) It is not possible to construct a ΔABC given that BC = 7 cm, ∠B = 45° and AB – AC = 10 cm.
(iii) We can construct an angle of 67.5° using ruler and compass.
(iv) Construction of ΔDEF, if EF = 5.5 cm, ∠E = 75° and DE – DF = 3 cm is possible.
Answer: (i) Yes, because 22.5° = 45° ÷ 2 and 45° can be constructed.
(ii) Yes, it is not possible to construct a ΔABC in which BC = 7 cm and AB – AC = 10 cm with ∠B = 45° because the difference between the given two sides is not less than the third side.
(iii) Yes, we can construct an angle of 67.5°, because 67.5° = 135° ÷ 2 and 135° = 90° + 45°, which can be constructed.
(iv) Yes, it is possible to construct a ΔDEF in which EF = 5.5 cm, ∠E = 75° and DE – DF = 3 cm because the difference between the given two sides is less than the third side.
| CBSE Class 9 Mathematics Coordinate Geometry Worksheet |
| CBSE Class 9 Mathematics Coordinate Geometry Worksheet Set B |
| CBSE Class 9 Mathematics Euclids Geometry Worksheet Set A |
| CBSE Class 9 Mathematics Euclids Geometry Worksheet Set B |
| CBSE Class 9 Mathematics Circles Worksheet Set A |
| CBSE Class 9 Mathematics Circles Worksheet Set B |
| CBSE Class 9 Mathematics Circles Worksheet Set C |
| CBSE Class 9 Mathematics Area Of Triangles Herons Formula Worksheet Set A |
| CBSE Class 9 Mathematics Statistics Worksheet Set A |
| CBSE Class 9 Mathematics Statistics Worksheet Set B |
Important Practice Resources for Class 9 Mathematics
CBSE Mathematics Class 9 Chapter 11 Constructions Worksheet
Students can use the practice questions and answers provided above for Chapter 11 Constructions to prepare for their upcoming school tests. This resource is designed by expert teachers as per the latest 2026 syllabus released by CBSE for Class 9. We suggest that Class 9 students solve these questions daily for a strong foundation in Mathematics.
Chapter 11 Constructions Solutions & NCERT Alignment
Our expert teachers have referred to the latest NCERT book for Class 9 Mathematics to create these exercises. After solving the questions you should compare your answers with our detailed solutions as they have been designed by expert teachers. You will understand the correct way to write answers for the CBSE exams. You can also see above MCQ questions for Mathematics to cover every important topic in the chapter.
Class 9 Exam Preparation Strategy
Regular practice of this Class 9 Mathematics study material helps you to be familiar with the most regularly asked exam topics. If you find any topic in Chapter 11 Constructions difficult then you can refer to our NCERT solutions for Class 9 Mathematics. All revision sheets and printable assignments on studiestoday.com are free and updated to help students get better scores in their school examinations.
You can download the latest chapter-wise printable worksheets for Class 9 Mathematics Chapter Chapter 11 Constructions for free from StudiesToday.com. These have been made as per the latest CBSE curriculum for this academic year.
Yes, Class 9 Mathematics worksheets for Chapter Chapter 11 Constructions focus on activity-based learning and also competency-style questions. This helps students to apply theoretical knowledge to practical scenarios.
Yes, we have provided solved worksheets for Class 9 Mathematics Chapter Chapter 11 Constructions to help students verify their answers instantly.
Yes, our Class 9 Mathematics test sheets are mobile-friendly PDFs and can be printed by teachers for classroom.
For Chapter Chapter 11 Constructions, regular practice with our worksheets will improve question-handling speed and help students understand all technical terms and diagrams.

