CBSE Class 9 Mathematics Probability Worksheet Set 03

Question: In a single throw of two dice, find the probability that there will be a doublet.
Answer: Number of elements in sample space when two dice are thrown = 6 × 6 = 36
Doublets are {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}
i.e., 6 in number
∴ P(getting doublet)
= Number of doublets/Number of elements in sample space
= 6/36 = 1/6

Question: The following table shows the birth months of 48 babies in a hospital: 

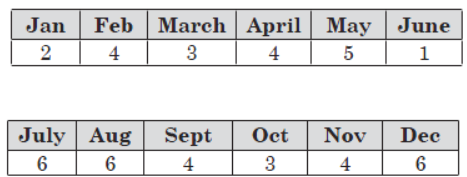
Find the probability of months in which 6 babies were born.
Answer: Number of months = 12 ⇒ n(S) = 12
Let E be the event having months in which 6 babies were born i.e., July, Aug and Dec
⇒ n(E) = 3
∴ P E = n(E)/n(S) = 3/12 = 1/4

Question: A survey of 100 children of a locality shows their favourite sport 

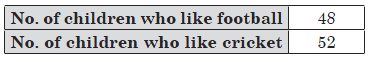
Out of these children, one is chosen at random.
What is the probability that the chosen child likes football?
Answer: Total number of students, n(S) = 100
Let E be the event that child likes football.
i.e., n(E) = 48
∴ P(E) = 48/100 = 12/25

Question: Based on the given information, find the probability of people with age 60, 61 & 64 who can drive.

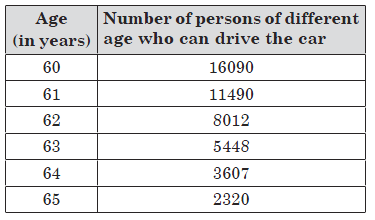
Answer: Number of people with age 60, 61 and 64 who can drive = 16090 + 11490 + 3607 = 31187
Total number of people who can drive
= 16090 + 11490 + 8012 + 5448 + 3607 + 2320 = 46967
∴ Required probability = 31187/46967

Question: The following data represents the number of girls in a family.

A family is chosen at random. Find the probability of having exactly 2 girls in the chosen family.
Answer: Total number of families = 1000 = n(S)
Number of families having exactly 2 girls = 475 = n(E)
∴ P E = n(E)/n(S) = 475/1000 = 19/40

Short Answer Type Questions:

Question: The number of hours spent by Ashu, a school student, on various activities on a working day are given below:

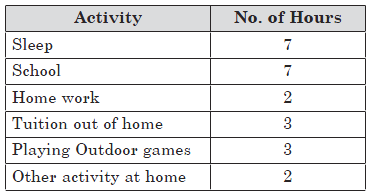
His friend Sonu came to his house to meet Ashu.
What is the probability that
(i) Ashu is available at home.
(ii) Ashu will play outdoor games.
Answer: Total number of hours = 24
(i) Number of hours during which Ashu is at home 
= 7 + 2 + 2 = 11
∴ Probability that Ashu is available at home = 11/24
(ii) Number of hours during which Ashu plays outdoor games = 3
∴ Probability that Ashu will play outdoor games = 3/24 = 1/8

Question: An integer is chosen at random from the first 200 positive integers. Find the probability that the integer is divisible by 11.
Answer: Total number of integers in the sample space = 200 = n(S).
Among first 200 positive integers, we have 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132, 143, 154, 165, 176, 187, 198 are divisible by 11.
∴ Number of integers which are divisible by 11 = 18 
P(integer is divisible by 11)
= Number of integers divisible by 11/Total number of integers in sample space
= 18/200 = 9/100

Question: In a locality of 5000 families a survey was conducted and the following data was collected. 

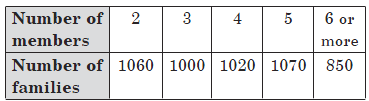
Out of these families, a family is chosen at random. What is the probability that the chosen family has less than 5 members?
Answer: Total number of families, n(S) = 5000
Let E be the event that the chosen family has less than 5 members.
i.e., n(E) = 1060 + 1000 + 1020 = 3080
∴ P(E) = n(E)/n(S) = 3080/5000 = 77/125

Question: The percentage of attendance of different classes in a year in a school is given below: 

(i) What is the probability that the class attendance is more than 75%?
(ii) Find the probability that the class attendance is less than 50%.
Answer: Total number of classes = 6
(i) Number of classes in which attendance percentage is more than 75% = 3
∴ Required probability = 3/6=1/2
(ii) Number of classes in which attendance is less than 50% = 1
∴ Required probability = 1/6

Question: In 60 throws of a die, the outcomes were noted as below:

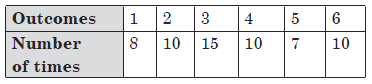
If die is thrown at random, then what is the probability that upper face of a die shows an even prime number? Also find the probability that upper face shows an odd number.
Answer: Total number of throws, n(S) = 60
Let E be the event that upper face shows an even prime number, i.e.,
n(E) = 10 [ 2 is the only even prime number]
∴ P(E) = n(E)/n(S) = 100/60 = 1/6 
Let F be the event that upper face shows an odd number
= 8 + 15 + 7 = 30
∴ P(F) = n(F)/n(S) = 30/60 = 1/2

Question: There are 35 students in class IX–A, 34 in IX-B and 33 in IX–C. Some of them are allotted project on Chapter 2 (Polynomials) and some on Chapter-1 (Number system) as shown in the table.

Find the probability that the student chosen at random,
(i) prepares project on chapter 1
(ii) prepares project on chapter 2
Answer: Total number of students = 35 + 34 + 33 = 102
(i) Number of students prepare project on chapter-1 = 74
∴ Probability that the student prepares project on
chapter-1 = 74/102 = 37/51
(ii) Number of students prepare project on chapter-2 = 28
∴ Probability that the student prepares project on
chapter-2 = 28/102 = 14/51

Question: A die was rolled 100 times and the number of times, 6 came up was noted. If the experimental probability calculated from this information is 2/5 , then how many times 6 came up?
Answer: Here, total number of trials = 100 
Let x be the number of times 6 came up.
We know, probability of an event
= Frequency of the event occuring/Total number of trials 
⇒ x/100 = 2/5
⇒ x = 40

Question: The probability of guessing the correct answer to a certain question is x/5 . If the probability of not
guessing the correct answer is 2x/3 . Then, find the value of 26x.
Answer: We have
P(guessing correct answer) = x/5 and P(not guessing correct answer) = 2x/3
Clearly, P(guessing correct answer) + P(not guessing correct answer) = 1 [ P(E) + P (not E) = 1]
∴ x/5 + 2x/3 = 1
⇒ 3x + 10x = 15 ⇒ x = 15/13 ⇒ 26x = 26 x 15/13 = 30

Question: A die is thrown 100 times and following observations were recorded:

Find the probability that the die shows
(i) a number less than 3.
(ii) a number greater than 4.
Answer: n(S) = 100
(i) Let E be the event that the die shows a number less than 3, i.e., n(E) = 12 + 18 = 30
∴ P(E) = n(E)/n(S) = 30/100 = 3/10
(ii) Let F be the event that the die shows a number greater than 4, i.e., n(F) = 14 + 16 = 30
∴ P(F) = n(F)/n(S) = 30/100 = 3/10

Question: If the difference between the probability of success and failure (i.e., not success) of an event
is 5/19 (assuming probability of failure is greater than that of success). Find the probability of success and failure of the event respectively. 
Answer: Let the probability of success be x
Then, probability of failure = 1 – probability of success
⇒ Probability of failure = 1 – x
According to question, we have,
Probability of failure – Probability of success = 5/19
⇒ 1 − x − x = 5/19 ⇒ 1−2x = 5/19
⇒ 2x = 1 − 5/19 = 14/19 ⇒ x=7/19
∴ Probability of success = 7/19
and probability of failure = 1 − 7/19 = 12/19

Long Answer Type Questions:

Question: Sixty seeds were selected at random from each of 8 bags of seeds, and were kept under standardised conditions favourable to germination. After 1 month, the number of seeds which had germinated in each collection were counted and recorded as follows :

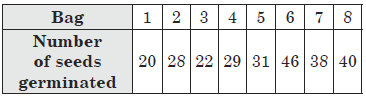
What is the probability of germination of
(i) more than 30 seeds in a bag ?
(ii) 50 seeds in a bag ?
(iii) less than 30 seeds in a bag ?
Answer: Total number of bags = 8
(i) Number of bags in which more than 30 seeds germinated = 4
∴ P(germination of more than 30 seeds in a bag) = 4/8 = 1/2
(ii) Number of bags in which 50 seeds germinated = 0 
∴ P(germination of 50 seeds in a bag) = 0/8 = 0
(iii) Number of bags in which less than 30 seeds germinated = 4
∴ P(germination of less than 30 seeds in a bag) = 4/8 = 1/2

Question: Given below is the frequency distribution of daily wages (in Rs) of 30 workers in a certain factory.

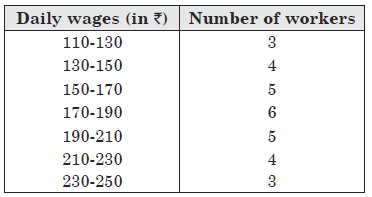
A worker is selected at random. Find the probability that his wages is
(i) less than Rs 150
(ii) atleast Rs 210
(iii) more than or equal to Rs 150 but less than Rs 210
(iv) in the interval 190-250
Answer: The total number of workers = 30
(i) Number of workers whose wages are less than Rs 150
= 3 + 4 = 7
∴ P(that worker get wages less than Rs 150) = 7/30
(ii) Number of workers whose wages are atleast Rs 210
= 4 + 3 = 7
∴ P(that worker get wages atleast Rs 210) = 7/30
(iii) Number of workers whose wages are more than or equal to Rs 150 but less than Rs 210 = 5 + 6 + 5 = 16
∴ P(that worker get wages more than or equal to Rs 150 but less than Rs 210) = 16/30 = 8/15
(iv) Number of workers whose wages lie in the interval 190-250 = 5 + 4 + 3 = 12
∴ P(that worker get wages lie in the interval 190-250) = 12/30 = 2/5.

Question 1. Three coins are tossed once, find the probability of getting at least one head (7/8)
Answer: When three fair coins are tossed at the same time, the sample space of all possible results is given by:
\( S = \{ HHH, HHT, HTH, HTT, THH, THT, TTH, TTT \} \)
Total number of elementary outcomes: \( n(S) = 2^3 = 8 \).
Let \( E \) denote the event of obtaining at least one head. The favorable combinations include any outcome with one, two, or three heads:
\( E = \{ HHH, HHT, HTH, HTT, THH, THT, TTH \} \)
Number of favorable outcomes: \( n(E) = 7 \).
Therefore, the probability of getting at least one head is:
\( P(E) = \frac{n(E)}{n(S)} = \frac{7}{8} \)
In simple words: Out of the 8 total ways three coins can land, 7 outcomes contain one or more heads, which gives a 7 in 8 chance.

Exam Tip: For "at least one" problems, compute the complement \( 1 - P(\text{no heads}) = 1 - \frac{1}{8} = \frac{7}{8} \) to quickly verify your final fraction.

Question 2. Three coins are tossed simultaneously 200 times with the following frequencies of different Outcomes:

Find the probability of getting:
(a) 2 Heads (9/25)
(b) at least 2 Heads (19/40)
Answer: Total count of coin tosses: \( n = 200 \).

(a) The frequency of turning up exactly 2 heads is 72.
\( P(\text{getting 2 Heads}) = \frac{72}{200} = \frac{9}{25} \)

(b) The condition "at least 2 heads" encompasses outcomes with either 2 heads or 3 heads.
Number of favorable trials = \( 72 + 23 = 95 \).
\( P(\text{getting at least 2 Heads}) = \frac{95}{200} = \frac{19}{40} \)
In simple words: Divide the matching tally from the table by 200, then simplify the fraction to its lowest terms.

Exam Tip: Remember that "at least 2" means 2 or more, so you must add the frequency of 2 heads and 3 heads together.

Question 3. A dice is thrown once, find the probability of getting a prime number (1/2)
Answer: The set of possible results when rolling a standard die once is:
\( S = \{ 1, 2, 3, 4, 5, 6 \} \), meaning total outcomes \( n(S) = 6 \).
The prime numbers present in this range are 2, 3, and 5 (note that 1 is neither prime nor composite).
Favorable outcomes: \( \{ 2, 3, 5 \} \), so \( n(E) = 3 \).
Hence, the required probability is:
\( P(\text{prime number}) = \frac{3}{6} = \frac{1}{2} \)
In simple words: Three of the six faces on a die show prime numbers, which simplifies to a probability of 1 in 2.

Exam Tip: Never include 1 among prime numbers; the primes on a normal die are exclusively 2, 3, and 5.

Question 4. A dice is thrown once. Find the probability of getting:
(a) An even number (1/2)
(b) A prime number (1/2)
(c) A number greater than 4 (1/3)
Answer: The complete sample space for a single die roll is \( S = \{ 1, 2, 3, 4, 5, 6 \} \), giving \( n(S) = 6 \).

(a) Even numbers on a die are 2, 4, and 6.
Number of favorable cases = 3.
\( P(\text{even number}) = \frac{3}{6} = \frac{1}{2} \)

(b) Prime numbers among these values are 2, 3, and 5.
Number of favorable cases = 3.
\( P(\text{prime number}) = \frac{3}{6} = \frac{1}{2} \)

(c) The values strictly greater than 4 are 5 and 6.
Number of favorable cases = 2.
\( P(\text{number greater than 4}) = \frac{2}{6} = \frac{1}{3} \)
In simple words: Count how many faces match each requirement and place that count over the 6 total faces of the die.

Exam Tip: Pay close attention to "greater than 4" versus "greater than or equal to 4"; strictly greater does not include 4 itself.

Question 5. A fair die is tossed once. Find the probability of getting:
(a) a number more than or equal to 3 ( 2/3)
(b) a multiple of 3 (1/3)
Answer: The full list of outcomes for rolling a fair die is \( \{ 1, 2, 3, 4, 5, 6 \} \), so \( n(S) = 6 \).

(a) Numbers that are greater than or equal to 3 are 3, 4, 5, and 6.
Favorable outcomes count = 4.
\( P(\text{number } \ge 3) = \frac{4}{6} = \frac{2}{3} \)

(b) Numbers that are multiples of 3 on a die are 3 and 6.
Favorable outcomes count = 2.
\( P(\text{multiple of 3}) = \frac{2}{6} = \frac{1}{3} \)
In simple words: There are 4 numbers that are 3 or bigger giving 4/6, and 2 numbers divisible by 3 giving 2/6.

Exam Tip: Always reduce fractions like \( \frac{4}{6} \) and \( \frac{2}{6} \) to their lowest terms to secure full credit.

Question 6. A letter of English alphabet is choosen at random. Calculate the probability that the letter choosen is a vowel ( 5/26)
Answer: The English alphabet contains a total of 26 letters, which defines the total number of possible outcomes: \( n(S) = 26 \).
The vowels in the alphabet are A, E, I, O, and U.
Total count of favorable vowels: \( n(E) = 5 \).
Thus, the probability of selecting a vowel is:
\( P(\text{vowel}) = \frac{n(E)}{n(S)} = \frac{5}{26} \)
In simple words: With 5 vowels out of 26 total letters, picking one at random gives a probability of 5/26.

Exam Tip: In standard English probability questions, consider only the 5 primary vowels (A, E, I, O, U) unless explicitly stated otherwise.

Question 7. A bag contains 15 balls numbered 1 to 15. Find the probability of drawing a prime number, When one ball is drawn from the bag at random (2/5)
Answer: The collection of balls is numbered from 1 through 15, providing a total of 15 possible outcomes: \( n(S) = 15 \).
The prime numbers in the set \( \{ 1, 2, 3, \dots, 15 \} \) are 2, 3, 5, 7, 11, and 13.
Total count of prime-numbered balls: \( n(E) = 6 \).
Therefore, the probability of pulling a prime number is:
\( P(\text{prime number}) = \frac{6}{15} = \frac{2}{5} \)
In simple words: There are 6 prime numbers up to 15, so the chance is 6 out of 15, which reduces to 2/5.

Exam Tip: List prime numbers systematically (2, 3, 5, 7, 11, 13) so that you neither omit composite numbers nor accidentally include 1 or 9.

Question 8. Marks obtained by 50 students in a class test of 100 marks are given below :

Find the probability that a student obtained less than 50% marks ( 8/25 )
Answer: Total number of assessed students: \( n(S) = 50 \).
Since the examination is out of 100 marks, achieving less than 50% marks corresponds to scoring under 50 marks.
The intervals below 50 are \( 0 - 25 \) and \( 25 - 50 \).
Number of students scoring less than 50 marks = \( 4 + 12 = 16 \).
Therefore, the probability is:
\( P(\text{marks } < 50\%) = \frac{16}{50} = \frac{8}{25} \)
In simple words: Exactly 16 students scored below 50 marks, so dividing 16 by 50 gives 8/25.

Exam Tip: First translate percentages into actual marks based on the maximum test score before reading values off the frequency table.

Question 9. In a one day international cricket match , a batsman played 40 balls. The runs scored as Follows

Find the probability that the batsmen will score :
(a) 6 runs ( 1/20)
(b) A four or a six run (3/20)
Answer: Total number of deliveries faced by the batsman: \( n(S) = 40 \).

(a) Balls resulting in 6 runs = 2.
\( P(\text{scoring 6 runs}) = \frac{2}{40} = \frac{1}{20} \)

(b) Balls on which either a boundary (4 runs) or a sixer (6 runs) was struck = \( 4 + 2 = 6 \).
\( P(\text{scoring a four or a six}) = \frac{6}{40} = \frac{3}{20} \)
In simple words: Divide the balls matching the target run values by the total 40 balls faced and reduce the fractions.

Exam Tip: Be sure to sum the separate frequencies for 4s and 6s when computing the combined probability for part (b).

Question 10. One number is choosen at random from numbers 1 to 100. Find the probability that it is divisible by 4 or 6 (33/100)
Answer: The total count of numbers from 1 up to 100 is \( n(S) = 100 \).
Let \( A \) represent the event that the chosen number is divisible by 4, and \( B \) represent divisibility by 6.
Multiples of 4 in this set: \( \lfloor \frac{100}{4} \rfloor = 25 \), so \( n(A) = 25 \).
Multiples of 6 in this set: \( \lfloor \frac{100}{6} \rfloor = 16 \), so \( n(B) = 16 \).
Numbers divisible by both 4 and 6 are multiples of their least common multiple, \( \text{LCM}(4, 6) = 12 \).
Multiples of 12 in this range: \( \lfloor \frac{100}{12} \rfloor = 8 \), so \( n(A \cap B) = 8 \).
Applying the addition rule of sets:
\( n(A \cup B) = n(A) + n(B) - n(A \cap B) = 25 + 16 - 8 = 33 \)
Hence, the probability of selecting a number divisible by 4 or 6 is:
\( P(A \cup B) = \frac{33}{100} \)
In simple words: Add the counts of numbers divisible by 4 and 6, subtract the ones divisible by 12 counted twice, and put the result over 100.

Exam Tip: Always subtract the count of multiples of the LCM to prevent double-counting numbers that share both factors.

Question 11. In a survey of 80 people, 60 people like apple juice and remaining dislike it . Find the Probability that people dislike apple juice (1/4)
Answer: Total number of individuals surveyed: \( n(S) = 80 \).
Number of respondents who enjoy apple juice = 60.
Number of respondents who dislike apple juice: \( 80 - 60 = 20 \).
Consequently, the probability that a randomly chosen person dislikes apple juice is:
\( P(\text{dislike apple juice}) = \frac{20}{80} = \frac{1}{4} \)
In simple words: Taking away the 60 who like the juice leaves 20 who do not, which gives 20 out of 80, or 1/4.

Exam Tip: State the subtraction step \( 80 - 60 = 20 \) clearly to earn full method marks before writing down the final fraction.

Question 12. 250 families with 2 children are selected randomly and following data were obtained:

Find the probability of families having:
(a) 2 sons (3/10)
(b) 1 son (1/2)
(c) no son (1/5)
Answer: Total number of surveyed families: \( n(S) = 250 \).

(a) Families with 2 sons = 75.
\( P(\text{2 sons}) = \frac{75}{250} = \frac{3}{10} \)

(b) Families with 1 son = 125.
\( P(\text{1 son}) = \frac{125}{250} = \frac{1}{2} \)

(c) Families with no sons (0 sons) = 50.
\( P(\text{no son}) = \frac{50}{250} = \frac{1}{5} \)
In simple words: Divide the family count for each category by the overall 250 families and simplify each fraction.

Exam Tip: You can quickly check your arithmetic by verifying that the sum of the probabilities equals 1: \( \frac{3}{10} + \frac{5}{10} + \frac{2}{10} = 1 \).

Question 13. 1500 family with 2 children were selected randomly and the following data was recorded:

Compute probability of a family chosen at random having
(a) At most 1 girl (41/60)
(b) At least 2 girls (19/60)
Answer: Total number of selected families: \( n(S) = 1500 \).

(a) "At most 1 girl" indicates either 0 girls or 1 girl.
Favorable families = \( 211 + 814 = 1025 \).
\( P(\text{at most 1 girl}) = \frac{1025}{1500} = \frac{41}{60} \)

(b) "At least 2 girls" in a two-child family means exactly 2 girls.
Favorable families = 475.
\( P(\text{at least 2 girls}) = \frac{475}{1500} = \frac{19}{60} \)
In simple words: For at most 1 girl, add the counts for 0 and 1 girl; for at least 2 girls, take the count for 2 girls, then divide each by 1500.

Exam Tip: "At most" sets the upper limit, whereas "at least" defines the lower threshold; do not mix up which categories to combine.

Question 14. Probability of an impossible event is always………
(a) 0
(b) 1
(c) 2
(d) \( \frac{1}{2} \)
Answer: (a) 0
An impossible event is an outcome that cannot happen under any circumstances within the experiment. Because the number of favorable cases is zero, the probability is identically \( \frac{0}{n(S)} = 0 \).
In simple words: An event that can never occur has a chance of exactly zero.

Exam Tip: Remember the basic probability bounds: impossible events have probability 0, while certain events have probability 1.

Question 15. A die is thrown once. The probability of getting an even prime number is
(a) \( \frac{1}{2} \)
(b) \( \frac{1}{3} \)
(c) \( \frac{1}{6} \)
(d) \( \frac{2}{3} \)
Answer: (c) 1/6
The complete sample space when rolling a die is \( \{ 1, 2, 3, 4, 5, 6 \} \). The only number in mathematics that is simultaneously even and prime is 2. Thus, exactly 1 favorable outcome exists out of 6, yielding a probability of \( \frac{1}{6} \).
In simple words: Since 2 is the single even prime number on the die, the probability of rolling it is 1 out of 6.

Exam Tip: 2 is the only even prime number in existence; do not confuse even numbers (2, 4, 6) with even prime numbers.

Question 16. A coin is tossed once then probability of getting head is
(a) 2
(b) 1
(c) \( \frac{1}{2} \)
(d) 3
Answer: (c) 1/2
A single coin toss yields two equally likely possibilities: a Head or a Tail. With 1 favorable outcome out of 2 possible outcomes, the probability is \( \frac{1}{2} \).
In simple words: A fair coin has two equal sides, so landing on heads happens half the time.

Exam Tip: Any probability value greater than 1 is impossible, allowing you to instantly rule out options (a) and (d).

Question 17. There are 10 bulbs in a bag in which 4 bulbs are good and rest are fused, then the Probability of fused bulbs is
(a) \( \frac{3}{5} \)
(b) \( \frac{2}{5} \)
(c) 1
(d) \( \frac{2}{3} \)
Answer: (a) 3/5
Total bulbs available = 10. Since 4 bulbs are functional, the number of defective (fused) bulbs is \( 10 - 4 = 6 \). The probability of drawing a fused bulb is \( \frac{6}{10} = \frac{3}{5} \).
In simple words: Subtracting 4 good bulbs leaves 6 fused bulbs, giving a probability of 6/10, which reduces to 3/5.

Exam Tip: Check whether the question asks for the probability of good bulbs or fused bulbs before choosing your answer.

Question 18. Sum of the probability of happening and not happening of an event is
(a) 1
(b) 2
(c) 0
(d) None of the options
Answer: (a) 1
For any arbitrary event \( E \), the event occurring and its complementary event \( \bar{E} \) cover all possibilities without overlap. Hence, the relation \( P(E) + P(\bar{E}) = 1 \) holds universally.
In simple words: Something either happens or it does not happen, meaning the two chances combined always equal 1.

Exam Tip: Keep the identity \( P(E) + P(\text{not } E) = 1 \) in mind; it is frequently used to simplify complementary probability problems.

Question 19. The probability of winning a game is 0.3. Then, the probability of losing a game is
(a) 0.3
(b) 0.7
(c) 0.6
(d) 0.1
Answer: (b) 0.7
Winning and losing represent mutually exclusive complementary outcomes. Thus, the probability of defeat is determined by subtracting the chance of winning from 1: \( P(\text{losing}) = 1 - P(\text{winning}) = 1 - 0.3 = 0.7 \).
In simple words: Subtracting the winning chance of 0.3 from the whole amount of 1 leaves a 0.7 chance of losing.

Exam Tip: Use complementary probability \( P(E') = 1 - P(E) \) whenever an experiment has only two opposing outcomes.

Question 20. The Probability of a sure event is
(a) 1
(b) -1
(c) 0
(d) None of the options
Answer: (a) 1
A sure or certain event is guaranteed to happen because every elementary outcome in the sample space satisfies its condition. Therefore, its probability is always 1.
In simple words: An event that is guaranteed to take place has a probability equal to 1.

Exam Tip: Probabilities can never take negative values or exceed 1; a sure event always sits at the maximum possible value of 1.

Question 21. Out of 35 students participating in a debate 10 are girls. The probability that winner is a boy is :
(a) \( \frac{1}{7} \)
(b) \( \frac{3}{7} \)
(c) \( \frac{4}{7} \)
(d) \( \frac{5}{7} \)
Answer: (d) 5/7
Total students taking part: \( n(S) = 35 \).
With 10 female participants, the number of male participants is \( 35 - 10 = 25 \).
Assuming each participant has an equal chance, the probability that the winner is a boy is:
\( P(\text{boy wins}) = \frac{25}{35} = \frac{5}{7} \)
In simple words: There are 25 boys competing out of 35 students, giving a winning chance of 25/35, which simplifies to 5/7.

Exam Tip: Ensure you subtract girls from the total pool to find the number of boys before setting up your fraction.

Question 22. Which of the following cannot be the probability of an event
(a) \( \frac{1}{5} \)
(b) 0.3
(c) 4%
(d) \( \frac{5}{4} \)
Answer: (d) 5/4
The probability of any random event \( E \) is strictly restricted to the range \( 0 \le P(E) \le 1 \). Because \( \frac{5}{4} = 1.25 \) is strictly greater than 1, it cannot serve as a valid probability measure.
In simple words: A probability can never be more than 1 or 100%, so 5/4 (which equals 1.25) cannot be a probability.

Exam Tip: An improper fraction where the numerator exceeds the denominator evaluates to greater than 1 and is never a valid probability.

Question 23. In a cricket match, a batsman hits a sixer 8 times out of 32 balls played. The probability that a sixer is not hit in a ball is :
(a) 0.75
(b) 0.25
(c) -0.25
(d) 0.5
Answer: (a) 0.75
Total balls faced = 32.
Deliveries where a six was struck = 8.
Deliveries without a six = \( 32 - 8 = 24 \).
Therefore, the probability of not hitting a six on a given ball is:
\( P(\text{no six}) = \frac{24}{32} = \frac{3}{4} = 0.75 \)
In simple words: The batsman missed hitting a six on 24 of the 32 deliveries, which gives 24/32 or 0.75.

Exam Tip: You can also find this by taking the complement: \( 1 - \frac{8}{32} = 1 - 0.25 = 0.75 \).