Refer to CBSE Class 12 Mathematics Linear Programming MCQs Set A provided below available for download in Pdf. The MCQ Questions for Class 12 Mathematics with answers are aligned as per the latest syllabus and exam pattern suggested by CBSE, NCERT and KVS. Chapter 12 Linear Programming Class 12 MCQ are an important part of exams for Class 12 Mathematics and if practiced properly can help you to improve your understanding and get higher marks. Refer to more Chapter-wise MCQs for CBSE Class 12 Mathematics and also download more latest study material for all subjects
MCQ for Class 12 Mathematics Chapter 12 Linear Programming
Class 12 Mathematics students should refer to the following multiple-choice questions with answers for Chapter 12 Linear Programming in Class 12.
Chapter 12 Linear Programming MCQ Questions Class 12 Mathematics with Answers
Question. The region represented by the inequalities x ≥ 6, y ≥ 2, 2x + y ≤ 0, x ≥ 0, y ≥ 0 is
(a) unbounded
(b) a polygon
(c) exterior of a triangle
(d) none of the options
Answer: d
Question. The minimum value of Z = 4x + 3y subjected to the constraints 3x + 2y ≥ 160, 5 + 2y ≥ 200, 2y ≥ 80; x, y ≥ 0 is
(a) 220
(b) 300
(c) 230
(d) none of the options
Answer: a
Question. The maximum value of f = 4x + 3y subject to constraints x ≥ 0, y ≥ 0, 2x + 3y ≤ 18; x + y ≥ 10 is
(a) 35
(b) 36
(c) 34
(d) none of the options
Answer: d
Question. Objective function of a L.P.P. is
(a) a constant
(b) a function to be optimised
(c) a relation between the variables
(d) none of the options
Answer: b
Question. Maximize Z = 11x + 8y, subject to x ≤ 4, y ≤ 6, x ≥ 0, y ≥ 0.
(a) 44 at (4, 2)
(b) 60 at (4, 2)
(c) 62 at (4, 0)
Answer: b
Question. The optimal value of the objective function is attained at the points
(a) on x-axis
(b) on y-axis
(c) which are corner points of the feasible region
(d) none of the options
Answer: c
Question. Z = 4x1 + 5x2, subject to 2x1 + x2 ≥ 7, 2x1 + 3x2 ≤ 15, x2 ≤ 3, x1, x2 ≥ 0. The minimum value of Z occurs at
(a) (3.5, 0)
(b) (3, 3)
(c) (7.5, 0)
(d) (2, 3)
Answer: a
Question. Minimize Z = 20x1 + 9x2, subject to x1 ≥ 0, x2 ≥ 0, 2x1 + 2x2 ≥ 36, 6x1 + x2 ≥ 60.
(a) 360 at (18, 0)
(b) 336 at (6, 4)
(c) 540 at (0, 60)
(d) 0 at (0, 0)
Answer: b
Question. Z = 8x + 10y, subject to 2x + y ≥ 1, 2x + 3y ≥ 15, y ≥ 2, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4.5, 2)
(b) (1.5, 4)
(c) (0, 7)
(d) (7, 0)
Answer: b
Question. In solving the LPP: “minimize f = 6x + 10y subect to constraints x ≥ 6, y ≥ 2, 2x + y ≥ 10, x ≥ 0, y ≥ 0” redundant constraints are
(a) x ≥ 6, y ≥ 2
(b) 2x + y ≥ 10, x ≥ 0, y ≥ 0
(c) x ≥ 6
(d) none of the options
Answer: b
Question. Region represented by x ≥ 0, y ≥ 0 is
(a) first quadrant
(b) second quadrant
(c) third quadrant
(d) fourth quadrant
Answer: a
Question. The maximum value of Z = 3x + 2y, subjected to x + 2y ≤ 2, x + 2y ≥ 8; x, y ≥ 0 is
(a) 32
(b) 24
(c) 40
(d) none of the options
Answer: d
Question. Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + 4y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0.
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)
Answer: c
Question. Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0.
(a) 16 at (4, 0)
(b) 24 at (0, 4)
(c) 24 at (6, 0)
(d) 36 at (0, 6)
Answer: d
Case Based Questions
1. Linear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations.
Based on the above information, answer the following questions:
Question. The optimal value of the objective function is attained at the points
(a) on X-axis
(b) on Y-axis
(c) which are corner points of the feasible region
(d) none of the options
Answer: c
Question. The graph of the inequality 3x + 4y < 12 is
(a) half plane that contains the origin
(b) half plane that neither contains the origin nor the points of the line 3x + 4y = 12.
(c) whole XOY-plane excluding the points on line 3x + 4y = 12
(d) none of the options
Answer: d
Question. The corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20) is
(a) p = q
(b) p = 2q
(c) q = 2p
(d) q = 3p
Answer: d
2. Deepa rides her car at 25 km/hr. She has to spend ₹2 per km on diesel and if she rides it at a faster speed of 40 km/hr, the diesel cost increases to ₹5 per km. She has ₹100 to spend on diesel. Let she travels x kms with speed 25 km/hr and y kms with speed 40 km/hr. The feasible region for the LPP is shown below:
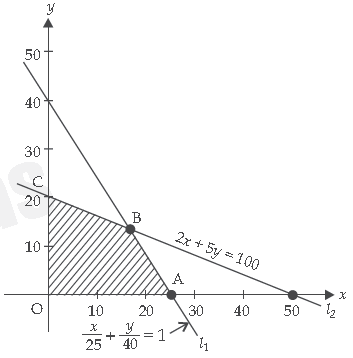
Based on the above information, answer the following questions:
Question. If Z = 6x – 9y be the objective function, then maximum value of Z is
(a) –20
(b) 150
(c) 180
(d) 20
Answer: b
Question. If Z = 6x + 3y be the objective function, then what is the minimum value of Z?
(a) 120
(b) 130
(c) 0
(d) 150
Answer: c
Corner points of the feasible region for an LPP are (0, 3), (5, 0), (6, 8), (0, 8). Let Z = 4x – 6y be the objective function.
Based on the above information, answer the following questions:
Question. The minimum value of Z occurs at
(a) (6, 8)
(b) (5, 0)
(c) (0, 3)
(d) (0, 8)
Answer: d
Question. Maximum value of Z occurs at
(a) (5, 0)
(b) (0, 8)
(c) (0, 3)
(d) (6, 8)
Answer: a
Question. Maximum of Z – Minimum of Z =
(a) 58
(b) 68
(c) 78
(d) 88
Answer: b
Question. The feasible solution of LPP belongs to
(a) first and second quadrant
(b) first and third quadrant
(c) only second quadrant
(d) only first quadrant
Answer: d
Suppose a dealer in rural area wishes to purpose a number of sewing machines. He has only ₹5,760 to invest and has space for at most 20 items for storage.

An electronic sewing machine costs him ₹360 and a manually operated sewing machine ₹240. He can sell an electronic sewing machine at a profit of ₹22 and a manually operated sewing machine at a profit of ₹18.
Based on the above information, answer the following questions:
Question. Let x and y denotes the number of electronic sewing machines and manually operated sewing machines purchased by the dealer. If it is assumed that the dealer purchased atleast one of the given machines, then
(a) x + y ≥ 0
(b) x + y < 0
(c) x + y > 0
(d) x + y ≤ 0
Answer: c
Question. Let the constraints in the given problem is represented by the following inequalities:
x + y ≤ 20
360x + 240y ≤ 5760
x, y ≥ 0
Then which of the following point lie in its feasible region.
(a) (0, 24)
(b) (8, 12)
(c) (20, 2)
(d) none of the options
Answer: b
Question. If the objective function of the given problem is maximise z = 22x + 18y, then its optimal value occur at
(a) (0, 0)
(b) (16, 0)
(c) (8, 12)
(d) (0, 20)
Answer: c
Question. If an LPP admits optimal solution at two consecutive vertices of a feasible region, then
(a) the required optimal solution is at the midpoint of the line joining two points.
(b) the optimal solution occurs at every point on the line joining these two points.
(c) the LPP under consideration is not solvable.
(d) the LPP under consideration must be reconstructed.
Answer: b
Let R be the feasible region (convex polygon) for a linear programming problem and let Z = ax + by be the objective function. When Z has an optimal value (maximum or minimum), where the variables x and y are subject to constraints described by linear inequalities, this optimal value must occur at a corner point (vertex) of the feasible region.
Based on the given information, answer the following questions:
Question. Objective function of a L.P.P. is
(a) a constant
(b) a function to be optimised
(c) a relation between the variables
(d) none of the options
Answer: b
Question. Which of the following statement is correct?
(a) Every LPP has at least one optimal solution
(b) Every LPP has a unique optimal solution.
(c) If an LPP has two optimal solutions, then it has infinitely many solutions.
(d) none of the options
Answer: c
Question. In solving the LPP : “minimize f = 6x + 10y subject to constraints x ≥ 6, y ≥ 2, 2x + y ≥ 10, x ≥ 0, y ≥ 0” redundant constraints are
(a) x ≥ 6, y ≥ 2
(b) 2x + y ≥ 10, x ≥ 0, y ≥ 0
(c) x ≥ 6
(d) none of the options
Answer: b
Question : In maximization problem, optimal solution occurring at corner point yields the
a) highest value of z
b) lowest value of z
c) mid values of z
d) mean values of z
Answer : A
Question : In a LPP, the objective function is always
a) Linear
b) Quadratic
c) Cubic
d) Biquadratic
Answer : A
Question : A feasible solution to a linear programming problem
a) Must satisfy all of the problem's constraints simultaneously
b) Need not satisfy all of the constraints, only the non-negativity constraints
c) Must be a corner point of the feasible region
d) Must give the maximum possible profit
Answer : A
Question : The corner points of the bounded feasible region of a LPP are A(0,50), B(20, 40), C(50, 100) and D(0, 200) and the objective function is Z = x + 2y. Then the maximum value is
a) 400
b) 250
c) 450
d) 100
Answer : A
Question : The feasible region (shaded) for a L.P.P is shown in the figure. The maximum Z = 5x + 7y is
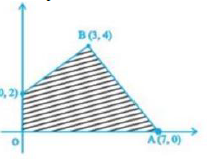
a) 43
b) 47
c) 45
d) 49
Answer : A
Attempt Mock Tests on this topic
| CBSE Class 12 Mathematics Determinants MCQs Set A |
| CBSE Class 12 Mathematics Indefinite and Definite Integrals MCQs |
| CBSE Class 12 Mathematics Application of Integrals MCQs Set A |
| CBSE Class 12 Mathematics Application of Integrals MCQs Set B |
| CBSE Class 12 Mathematics Linear Programming MCQs Set A |
| CBSE Class 12 Mathematics Linear Programming MCQs Set B |
| CBSE Class 12 Mathematics Case Study Problems MCQs |
MCQs for Chapter 12 Linear Programming Mathematics Class 12
Expert teachers of studiestoday have referred to NCERT book for Class 12 Mathematics to develop the Mathematics Class 12 MCQs. If you download MCQs with answers for the above chapter you will get higher and better marks in Class 12 test and exams in the current year as you will be able to have stronger understanding of all concepts. Daily Multiple Choice Questions practice of Mathematics will help students to have stronger understanding of all concepts and also make them expert on all critical topics. After solving the questions given in the MCQs which have been developed as per latest books also refer to the NCERT solutions for Class 12 Mathematics. We have also provided lot of MCQ questions for Class 12 Mathematics so that you can solve questions relating to all topics given in each chapter. After solving these you should also refer to Class 12 Mathematics MCQ Test for the same chapter.
You can download the CBSE MCQs for Class 12 Mathematics Chapter 12 Linear Programming for latest session from StudiesToday.com
Yes, the MCQs issued by CBSE for Class 12 Mathematics Chapter 12 Linear Programming have been made available here for latest academic session
You can find CBSE Class 12 Mathematics Chapter 12 Linear Programming MCQs on educational websites like studiestoday.com, online tutoring platforms, and in sample question papers provided on this website.
To prepare for Chapter 12 Linear Programming MCQs, refer to the concepts links provided by our teachers and download sample papers for free.
Yes, there are many online resources that we have provided on studiestoday.com available such as practice worksheets, question papers, and online tests for learning MCQs for Class 12 Mathematics Chapter 12 Linear Programming

