Refer to Class 11 Mathematics Sequences and Series MCQs Set C provided below available for download in Pdf. The MCQ Questions for Class 11 Mathematics with answers are aligned as per the latest syllabus and exam pattern suggested by CBSE, NCERT and KVS. Chapter 8 Sequences and Series Class 11 MCQ are an important part of exams for Class 11 Mathematics and if practiced properly can help you to improve your understanding and get higher marks. Refer to more Chapter-wise MCQs for CBSE Class 11 Mathematics and also download more latest study material for all subjects
MCQ for Class 11 Mathematics Chapter 8 Sequences and Series
Class 11 Mathematics students should refer to the following multiple-choice questions with answers for Chapter 8 Sequences and Series in Class 11.
Chapter 8 Sequences and Series MCQ Questions Class 11 Mathematics with Answers
Question: If 1, x, y, z, 16 are in geometric progression, then what is the value of x + y + z ?
a) 8
b) 12
c) 14
d) 16
Answer: c
Question: Let S1,S2…be squares such that for each n ≥1, the length of a side of Sn B,C, equals the length of a diagonal of Sn+1. If the length of a side of S1is 10cm, then for which of the following values of n is the area of Sn less 1sq cm2 than:
a) 7
b) 8
c) 9
d) 10
Answer: d
Question: If pth term of an AP is q, and its qth term is p, then what is the common difference ?
a) – 1
b) 0
c) 2
d) 1
Answer: a
Question: If a, b, c are in geometric progression and a, 2b,3c are in arithmetic progression, then what is the common ratio r such that 0 < r < 1 ?
a) 1/3
b) 1/2
c) 1/4
d) 1/8
Answer: a
Question: If 5 (3a – 1 + 1), (62a – 3 +2) and 7(5a – 2 + 5) are in AP, then what is the value of a?
a) 7
b) 6
c) 5
d) none
Answer: d
Question: In a Geometric Progression with first term a and common ratio r, what is the Arithmetic Mean of the first five terms?
a) a + 2r
b) a r2
c) a (r5 – 1)/[5(r – 1)]
d) a (r4 – 1)/[5(r – 1)]
Answer: c
Question: Let a =1 ⋅ 2 ⋅ 3 ⋅ 4 ⋅ 5. Then:
a) 55 ≥ a
b) 3 3 ≥ 5!
c) 55 ≥ 6a
d) None of the options
Answer: a,b
Question: Let x be one AM and g1 and g2 be two G.Ms between y and z. What is g13 + g23 equal to ?
a) xyz
b) xy2z
c) xyz2
d) 2xyz
Answer: d
Question: 1+ 3+ 7 +15 + 31+………. to n terms = ?
a) 2n+1 − n
b) 2n+1 − n−2
c) 2n − n−2
d) None of the options
Answer: b
Question: What is the sum of the first 50 terms of the series (1 × 3) + (3 × 5) + (5 × 7) + …. ?
a) 1,71,650
b) 26,600
c) 26,650
d) 26,900
Answer: a
Question: Let
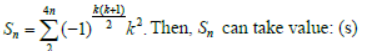
a) 1056
b) 1088
c) 1120
d) 1332
Answer: a,d
Question: If x + 1, 4x + 1, and 8x + 1 are in geometric progression, then what is the non-trivial value of x ?
a) – 1
b) 1
c) 1/8
d) 1/4
Answer: c
Question: The 10 th common term between the series 3 + 7 + 11 + …. and 1 + 6 + 11 + …. is
a) 191
b) 193
c) 211
d) None of the options
Answer: a
Question: If p, q, r are in a)P., a is G.M. between p and q and b is G.M. between q and r, then a2, q2, b2 are in G.P.
b) a)P.
c) H.P
d) None
Answer: b
Question: The sum of n terms of the series
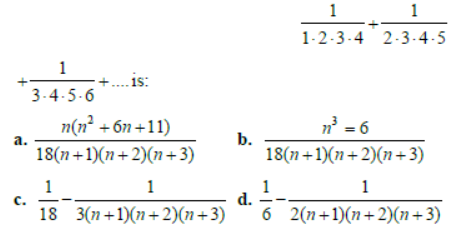
Answer: a,c
Question: Let bi > 1 for i = 1, 2,…,101. Suppos logeb1,logeb2,…logeb101 are in Arithmetic Progression (a.P.) with the common difference loge 2. Suppose a1,a2….a101 are in
a. P. such that a1=b1 and a51=b51.If t = b1 + b2 +…+ b51 and1 2 51 s = a + a +….+ a , then :
a) s > t anda101 > b101
b) s > t and a101 < b101
c) s < t and a101 > b101
d) s < t and a101 <b101
Answer: b
Assertion and Reason
Note: Read the Assertion (A) and Reason (R) carefully to mark the correct option out of the options given below:
a) If both assertion and reason are true and the reason is the correct explanation of the assertion.
b) If both assertion and reason are true but reason is not the correct explanation of the assertion.
c) If assertion is true but reason is false.
d) If the assertion and reason both are false.
e) If assertion is false but reason is true.
Question: The natural numbers are divided into rows as follows:

Assertion: Sum of the numbers in the 10th row is a number which can be written as sum of two cubes in two different ways.
Reason: Sum of the numbers in the rth row is
Answer: c
Question: Suppose a2,b2,c2 are in a.P.
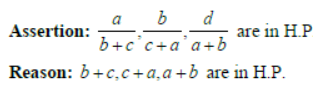
Answer: d
Question:
Assertion: The largest interval for which we can find the sum of the series +(2x−1) +(2x−1)2 +(2x−1)3 +… is (0, 1)
Reason: An infinite geometric series 2 a + ar + ar +… can be summed up if | r | <1.
Question:
Assertion: If a, b, c > 0 and the expression (a + c)x2
√(a + c)2 + 4b2 )x + b > 0 ∀ x∈R, then a,b,c are in G.P.
Reason: 2 ax + bx + c > 0 ∀ x∈R if and only if a > 0 and b2 − 4ac < 0.
Answer: d
Question: Let α ,β be roots of 2 ax + 2bx + c = 0 and 2 ) = b − ac)
Assertion: If α +β ,α2 + β2 ,α3 +β3 are in G.P. then c) = 0
Reason: If α ,αβ ,β are in a)P. then b + c = 0.
Answer: b
Question: Suppose four distinct positive numbers a1 ,a2 ,a3 ,a4 are in G.P.
Let b1 = a1 ,b2 = b1 + a2 ,b3 = b2 + a3 and b4 = b3 + a4 .
Assertion: The numbers b1 ,b2 ,b3 ,b4 are neither in a)P. nor in G.P.
Reason: The numbers b1 ,b2 ,b3 ,b4 are in H.P.
Answer: c
Question: Let a, b, c, d, e be five non-zero numbers such that a, b, c are in a)P., b, c, d are in G.P., and c, d, e are in H.P.?
Assertion: If a = 2,e =18,b > 0, then b = 4 and c = 6.
Reason: If a = 2,e =18,c = −6, then b < 0.
Answer: b
Question: Suppose a, b, c, d are four real number and
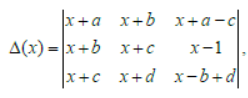
Assertion: If a, b, c, d are in a)P. and ∫02)△(x)dx = −4, then common difference of the a)P. is ± 1.
Reason: If a,b,c,d are in a)P., then △(x) is independent of x.
Answer: b
Question: Suppose four distinct positive numbers a1 , a2 ,a3 ,a4 are in
GP. Let b1 = a1 ,b2 = b1 + a2 ,b3 = b2 + a3 and b4 = b3 + a4
Assertion: The numbers b1 ,b2 ,b3 ,b4 are neither in AP nor in GP.
Reason: The numbers b1 ,b2 ,b3 ,b4 are in HP
Answer: c
Question:
Assertion: The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) is 800.
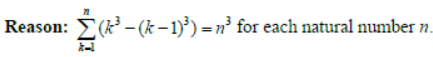
Answer: a
Paragraph –I
Let A1, G1, H1 denote the arithmetic, geometric and harmonic means, respectively, of two distinct positive numbers. For n ≥ 2,let An – 1 and Hn – 1 has arithmetic, geometric and harmonic means as An, Gn, Hn respectively.
Question: Which one of the following statements is correct ?
a) G1 > G2 > G3 > …
b) G1 < G2 , < G3 > …
c) G1 = G2 = G3 = …
d) G1 < G3 < G3 < … and G2 > G4 > G6 > …
Answer: a
Question: Which of the following statements is correct ?
a) A1 > A2 >…
b) A1 < A2 < A3 < ….
c) A1 > A3 > A5 > …. and A2 < A4 < A6 < ….
d) A1 < A3 < A5 < ….and A2 > A4 > A6 > ….
Answer: a
Question: Which of the following statements is correct ?
a) H1 > H2 > H3 > ….
b) H1 < H2 < H3 < ….
c) H1 > H3 > H5 > ….and H2 < H4 < H6 < ….
d) H1 < H3 < H5 < ….and H2 > H4 > H6 > ….
Answer: b
Paragraph –II
Let an denote the number of all n-digit positive integers formed by the digits 0, 1 or both such that no consecutive digits in them are 0. Let bn = The number of such n-digit integers ending with digit 1 and cn =
The number of such n-digit integers ending with digit 0.
Match the Column
Answer: If an+1 + bn+1/an + bn then:
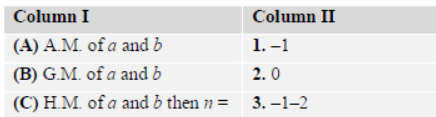
a) A→2 , B→3, C→1
b) A→1, B→2, C→3
c) A→3, B→2, C→1
d) A→3, B→1, C→2
Answer: a
Question: Match the statement of Column I with those in Column II:

a) A→4, B→1, C→5, D→3, E→2
b) A→4, B→2, C→3, D→5, E→1
c) A→2, B→3, C→5, D→1, E→4
d) A→ 5, B→ 1, C→4, D→3, E→2
Answer: b
Question: Which of the following is correct ?
a) a17 = a16 + a15
b) a17 ≠ a16 + a15
c) b17 ≠ b16 + c16
d) a17 = c16 + b16
Answer: a
Question: The value of b6 is:
a) 7
b) 8
c) 9
d) 11
Answer: b
Question: a, b, c∈R and a, b, c are in a)P. math the entries of column I with those of column II:

a) A→1, B→1, C→1.2.3, D→4
b) A→1, B→2, C→1.4.3, D→3
c) A→2, B→3, C→1.2.3, D→4
d) A→1, B→3, C→1.2.3, D→2
Answer: a
Question: If
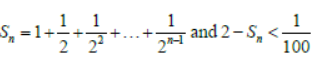
then the least value of n must be:
Answer: 8
Question: If (1) (2010) + (2) (2009) + (3) (2008) + . . .+ (2010) (1) = (335) (2011) (λ), then the value of λ must be:
Answer: 2021
Question: If
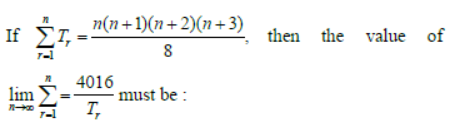
Answer: 2008
Question: If a, b, c are in HP and if (a+2b/2a−b) + (C+b/2c−b) > √λ√λ√λ…..∞ then the value of λ must be :
Answer: 4
Question: Let Sk, k = 1,2…100 denote the sum of the infinite geometric series whose first term is k–1/k! nd the common ratio is 1/k. Then the value of 1002/100!
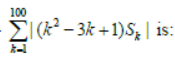
Answer: 4
Question: The minimum value of the sum of real numbers a−5 , a−4 , 3a−3 ,1, a8 and a10 a with a > 0 is:
Answer: 8
Question: A pack contains n card numbered from 1 to n. Two consecutive numbered card are removed from the pack and the sum of the numbers on the remaining cards is 1224. If the smaller of the numbers on the removed cards is k, then k – 20 is equal to:
Answer: 5
Question: Let a, b, c be positive integers such that b/a is an integer. If a,b, c are in geometric progression and the arithmetic mean of a, b, c is b + 2, then the value of a2 + a−14/a+1 is:
Answer: 4
Question: Let a1,a2,a3,…a11 be real numbers satisfying a1=15,27–2a2 > 0 and ak = 2ak−1−ak−2 for k = 3,4……11 IF a12 + a22 +…..a112 /11 = 90, then the value of a1+ a2+…..a11 / 11 is equal to:
Answer: 0
Question: Let a1 , a2 , a3 , …, a100 be an arithmetic progression with a1 = 3 and
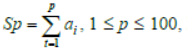
For any integer n with 1≤ n ≤ 20, let m = 5n. If Sm/Sn does not depend on n, then an is:
Answer: 3,9
Question:
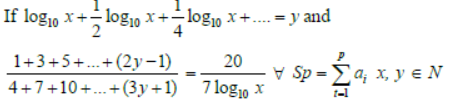
then the value of (logy x)5 must be :
Answer: 3125
Paragraph –III
Let r V denotes the sum of the first r terms of an arithmetic progression (AP) whose first term is r and the common difference is (2r – 1). Let Tr = Vr+1 − Vr − 2 = and Qr = Tr+1 − Tr = for r = 1, 2, …
Question: Tr is always:
a) an odd number
b) an even number
c) a prime number
d) a composite number
Answer: d
Question: Which one of the following is a correct statement?
a) Q1 , Q2, Q3,…are in AP with common difference 5
b) Q1 , Q2, Q3,…are in AP with common difference 6
c) Q1 , Q2, Q3,…are in AP with common difference 11
d) Q1 = Q2= Q3= …
Answer: b
| Class 11 Mathematics Set MCQs Set A |
| Class 11 Mathematics Set Theory MCQs Set A |
| Class 11 Mathematics Set Theory MCQs Set B |
| Class 11 Mathematics Relations and Functions MCQs Set A |
| Class 11 Mathematics Relations and Functions MCQs Set B |
| Class 11 Mathematics Relations and Functions MCQs Set C |
| Class 11 Mathematics Trigonometric Functions MCQs Set A |
| Class 11 Mathematics Trigonometric Functions MCQs Set B |
| Class 11 Mathematics Trigonometric Functions MCQs Set C |
| Class 11 Mathematics Probability MCQs Set A |
| Class 11 Mathematics Probability MCQs Set B |
| Class 11 Mathematics Probability MCQs Set C |
| Class 11 Mathematics Probability MCQs Set D |
MCQs for Chapter 8 Sequences and Series Mathematics Class 11
Expert teachers of studiestoday have referred to NCERT book for Class 11 Mathematics to develop the Mathematics Class 11 MCQs. If you download MCQs with answers for the above chapter you will get higher and better marks in Class 11 test and exams in the current year as you will be able to have stronger understanding of all concepts. Daily Multiple Choice Questions practice of Mathematics will help students to have stronger understanding of all concepts and also make them expert on all critical topics. After solving the questions given in the MCQs which have been developed as per latest books also refer to the NCERT solutions for Class 11 Mathematics. We have also provided lot of MCQ questions for Class 11 Mathematics so that you can solve questions relating to all topics given in each chapter. After solving these you should also refer to Class 11 Mathematics MCQ Test for the same chapter.
You can download the CBSE MCQs for Class 11 Mathematics Chapter 8 Sequences and Series for latest session from StudiesToday.com
Yes, the MCQs issued by CBSE for Class 11 Mathematics Chapter 8 Sequences and Series have been made available here for latest academic session
You can find CBSE Class 11 Mathematics Chapter 8 Sequences and Series MCQs on educational websites like studiestoday.com, online tutoring platforms, and in sample question papers provided on this website.
To prepare for Chapter 8 Sequences and Series MCQs, refer to the concepts links provided by our teachers and download sample papers for free.
Yes, there are many online resources that we have provided on studiestoday.com available such as practice worksheets, question papers, and online tests for learning MCQs for Class 11 Mathematics Chapter 8 Sequences and Series

