Exercise 1.1
Question 1: Is zero a rational number? Can you write it in the form p/q , where p and q are integers and q ≠ 0?
Solution 1:
Yes, zero is a rotational number. It can be written in the form of p/q where p and q are integers and q ≠ 0. For example: 0/2, 0/3, 0/5,0/7,……….
Question 2: Find five rational numbers between 1 and 2.
Solution 2:
Rational number lying between 1 and 2 are
Since we want five numbers, we write 1 and 2 as rational numbers with denominator 5+1.
We need 5 rational number so 5+1 = 6
Multiply numerator and denominator by 6
1/1 × 6/6 = 6/6 and 2/1 × 6/6 = 12/6
We know,
6/6 < 7/6 < 8/6 < 9/6 < 10/6 < 11/6 < 12/6
Hence, the required six rational numbers are
1< 7/6 < 8/6 < 9/6 < 10/6 < 11/6 < 2
1< 7/6 < 4/3 < 3/2 < 5/3 < 11/6 < 2
Question 3: Find six rational numbers between 3 and 4.
Solution 3:
Rational number lying between 3 and 4 are
Since we want six numbers, we write 3 and 4 as rational numbers with denominator 6+1.
We need 6 rational number so 6+1 = 7
Multiply numerator and denominator by 7
3/1 × 7/7 = 21/7 and 4/1 × 7/7 = 28/7
We know,
21/7 < 22/7 < 23/7 < 24/7 < 25/7 < 26/7 < 27/7 < 28/7
Hence, the required six rational numbers are
3 < 22/7 < 23/7 < 24/7 < 25/7 < 26/7 < 27/7 < 4
Question 4: Find five rational number between 3/5 and 4/5
Solution 4:
Rational number lying between 3/5 and 4/5 are
Since we want five numbers, we write 3/5 and 4/5 as rational number with denominator divisible by 5+1 = 6.
We need 5 rational number so 5+1 = 6
Multiply numerator and denominator by 6
3/5 × 6/6 = 18/30 and 4/5 × 6/6 = 24/30
We know,
18/30 < 19/30 < 20/30 < 21/30 < 22/30 < 23/30 < 24/30
Hence, the required six rational numbers are
3/5 < 19/30 < 20/30 < 21/30 < 22/30 < 23/30 < 4/5
3/5 < 19/30 < 2/3 < 21/30 < 11/15 < 23/30 < 4/5
Question 5: Are the following statements true or false? Give reason for your answer.
(i) Every whole number is a natural number.
(ii) Every integer is a rational number.
(iii) Every rational number is an integer.
(iv) Every natural number is a whole number.
(v) Every integer is a whole number.
(vi) Every rational number is a whole number.
Solution 5:
(i) False, because 0 is a whole number but not a natural number.
(ii) True, because every integer p can be expressed in the form p/1, and so it is a rational number.
(iii) False, because integer is a part of rational number, for example: 2/5 is not an integer.
(iv) True, because every natural number is a whole number. For example: 1,2,3,4……
(v) False, because negative numbers (example: -1,-2,-3……) are not whole number.
(vi) False, because rational numbers like 2/5, 3/5, 7/9,………. are not whole numbers.
Exercise 1.2
Question 1: Express the following rational number as decimals:
(i) 42/100 (ii) 327/500 (iii) 15/4
Solution 1:
(i) The rational we have 42/100
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
Hence, the decimal expiration of the rational number 42/100 is 0.420.
(ii) The rational we have 327/500
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
Hence, the decimal expiration of the rational number 327/500 is 0.654
(iii) The rational we have 15/4
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
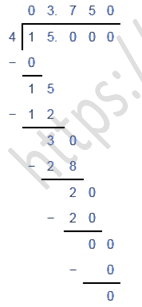
Hence, the decimal expiration of the rational number 15/4 is 03.750
Question 2: Express the following rational number as decimals:
(i) 2/3 (ii) - 4/9 (iii) - 2/15 (iv) - 22/13 (v) 437/999 (vi) 33/26
Solution 2:
(i) The rational we have 2/3
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
(ii) The rational we have - 4/9
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
(iii) The rational we have - 2/13
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
(iv) The rational we have - 22/13
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
(v) The rational we have 437/999
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-
(vi) The rational we have 33/26
We have to express this rational number in decimal expiration.
In long division method,
We can take numerator as dividend and denominator as divisor.
Below is the explanation of division:-

Question 3: Look at several examples of rational number in the form p/q (q≠0), where p and q are integers with no common factors other than 1 and having terminating decimal representations. Can you guess what property q must satisfy?
Solution 3:
2/5=0.4 5/2=2.5 3/5=0.6 5/8=0.625
The denominators of all the rational number are in the form of 2m × 5n, where m and n are integers. We can do the prime factorisation of denominators. We must have only the power of 2 or 5 or both.
Exercise 1.3
Question 1: Express each of the following decimals in the form p/q:
(i) 0.39 (ii) 0.750 (iii) 2.15 (iv) 7.010 (v) 9.90 (vi) 1.0001
Solution 1:
(i) We have 0.39
Now we have to convert decimal number into the form of p/q where q ≠ 0.
p/q = 0.39
Now we have to check there are two digits after the decimal. So, we put 100 in the denominator.
p/q = 39/100
Hence, 0.39 in the form of p/q is 39/100 Answer.
(ii) We have 0.750
Now we have to convert decimal number into the form of p/q where q ≠ 0.
p/q = 0.750
Now we have to check there are two digits after the decimal. So, we put 1000 in the denominator.
p/q = 750/1000
We can change it in standard form by dividing numerator and denominator by 250 = 3/4
Hence, 0.750 in the form of p/q is 3/4 Answer.
(iii) We have 2.15
Now we have to convert decimal number into the form of p/q where q ≠ 0.
p/q = 2.15
Now we have to check there are two digits after the decimal. So, we put 100 in the denominator.
p/q = 215/100
We can change it in standard form by dividing numerator and denominator by 5 = 43/20
Hence, 2.15 in the form of p/q is 43/20 Answer.
(iv) We have 7.010
Now we have to convert decimal number into the form of p/q where q ≠ 0.
p/q = 7.010
Now we have to check there are two digits after the decimal. So, we put 1000 in the denominator.
p/q = 7010/1000
We can change it in standard form by dividing numerator and denominator by 10 = 701/100
Hence, 7.010 in the form of p/q is 701/100 Answer.
(v) We have 9.90
Now we have to convert decimal number into the form of p/q where q ≠ 0.
p/q = 9.90
Now we have to check there are two digits after the decimal. So, we put 100 in the denominator.
p/q = 9.90/100
We can change it in standard form by dividing numerator and denominator by 10 = 99/10
Hence, 0.90 in the form of p/q is 99/10 Answer.
(vi) We have 1.0001
Now we have to convert decimal number into the form of p/q where q ≠ 0.
p/q = 1.0001
Now we have to check there are two digits after the decimal. So, we put 10000 in the denominator.
p/q = 1.0001/10000
Hence, 1.0001 in the form of p/q is 10001/10000 Answer.
Question 2: Express each of the following decimals in the form p/q:
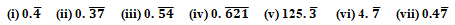





Exercise 1.4
Question 1: Define an irrational number.
Solution 1:
A number is called irrational number if it cannot be written in the form p/q, where p and q are integers and q ≠ 0. A real number that cannot be reduced to any ratio between an integer p and natural number q. For Example: √3 =1.732…….., √2 , √5, √(6 ) etc.
Question 2: Explain how irrational numbers differ from rational numbers?
Solution 2:
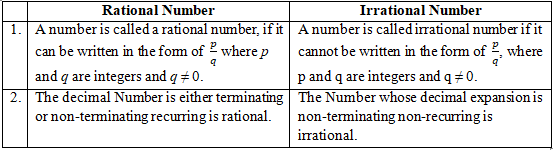
Question 3: Examine, whether the following number are rational or irrational:
(i) √7 (ii) √4 (iii) 2 + √3 (iv) √3 + √2 (v) √3 + √5 (vi) (√2 – 2)2 (vii) (2 – √2) (2 +√2) (viii) (√2 – √3)2 (ix) √5-2 (x) √23 (xi) √225 (xii) 0.3796 (xiii) 7.478478… (xiv) 1.101001000100001…..
Solution 3:
(i) Let us assumed x = √7
We know that √7 = 2.64575131……..
It is not a perfect square, but a non-terminating and non-repeating number.
Hence √7 is an irrational number.
(ii) Let us assumed x = √4
We know that √4 = 2
It is a perfect square and terminating.
Hence √4 is a rational number.
(iii) Let us assumed x = 2 + √3
We know that √3 = 1.732050807……..
x=2+1.732050807……….
x = 3.732050807……….
It is a non-terminating and non-repeating number.
Hence 2 + √3 is an irrational number.
(iv) Let us assumed x = √3+√2
We know that
√2 = 1.414213562…….
√3 = 1.732050807……..
√2 and √3 both are irrational number so there sum also an irrational number.
Hence √2 + √3 is an irrational number.
(v) Let us assumed x = √3+√5
We know that
√3 = 1.732050807……..
√5 = 2.236067977…….
√3 and √5 both are irrational number so there sum also an irrational number.
Hence √3 + √5 is an irrational number.
(vi) Let us assumed x = (√2-2)2
We know that (a-b)2 = a2 – 2ab + b2
x = (√2)2 – 2(√2) (2) + (2)2
x = 2 - 4√2 + 4
x = 6 - 4√2
Here √2 is an irrational number.
Hence (√2-2)2 is an irrational number.
(vii) Let us assumed x = (2-√2) (2+√2)
We know that a2 – b2 = (a+ b) (a- b)
x = (2)2 – (√2)2
x = 4 – 2
x = 2
It is a terminating number.
Hence (2-√2) (2+√2) is a rational number.
(viii) Let us assumed x = (√3+√2)2
We know that (a+b)2 = a2 + 2 ab + b2
x = (√3)2 + 2(√3) (√2) + (√2)2
x = 3 + 2√6 + 2
x = 5 + 4√2
Here √2 is an irrational number.
Hence (√3+√2)2 is an irrational number.
(ix) Let us assumed x = √5-2
We know that √5 = 2.236067977…….
x = 2.236067977………- 2
x = 0.236067977………
It is a non-terminating and non-repeating number or √5 is an irrational number. The sum and difference of a rational number and irrational number is always irrational.
Hence √3 + √5 is an irrational number.
(x) √23
Let us assumed x = √23
We know that √23 = 4.64575131……..
It is not a perfect square number, but a non-terminating and non-repeating number.
Hence √23 is an irrational number.
(xi) Let us assumed x = √225
We know that √225 = 15
It is a perfect square and terminating number.
Hence √225 is a rational number.
(xii) 0.3796
Given decimal number is terminating number. Hence 0.3796 is a rational number.
(xiii) 7.478478…….
Given decimal number is non-terminating number. Hence 7.478478….. is a irrational number.
(xiv) 1.101001000100001…..
Given decimal number is non-terminating number. Hence 1.101001000100001….. is a rational number.
Question 4. Identify the following as rational or irrational numbers. Give the decimal representation of rational number.
(i) √4 (ii) 3√(18 ) (iii) √1.44 (iv) √(9/27) (v) - √64 (vi) √100
Solution 4:
(i) Let us assumed x = √4
We know that √4 = 2
It is a perfect square and terminating.
Hence √4 is a rational number.
(ii) Let us assumed x = 3√18
We know that √18 = 4.24264068……..
It is not a perfect square number.
If we multiply 3 by the value of √18 we get a non-terminating and non-recurring number.
Hence 3√18 is an irrational number.
(iii) Let us assumed x = √1.44
x = √(144/100)
x = 12/10
x = 1.2
It is a perfect square and terminating.
Hence √1.44 is a rational number.
(iv) Let us assumed x = √(9/27)
x = 3/√27
x = 3/√(3 × 3 × 3)
x = 3/(3√(3 ))
x = 3/(3√(3 ))
x = 1/√(3 )
We know that √3 = 1.732050807……..
Here √3 is an irrational number.
Hence √(9/27) is an irrational number.
(v) Let us assumed x = - √64
We know that -√64 = - 8
It is a perfect square and terminating number.
Hence -√64 is a rational number.
(vi) Let us assumed x = √100
We know that √100 = 10
It is a perfect square and terminating number.
Hence √100 is a rational number.
Question 5: In the following equation, find which variables x, y, z etc. represent rational or irrational numbers:
(i) x2 = 5
(ii) y2 = 9
(iii) z2 = 0.04
(iv) u2 = 17/4
(v) v2 = 3
(vi) w2 = 27
(vii) t2 = 0.4
Solution 5:
(i) Given that x2 = 5
We know that
√5 = 2.236067977…….
It is not a perfect square number.
Hence x2 = 5 is an irrational number.
(ii) Given that y2 = 9
We know that √9 = 3
It is a perfect square number.
Hence y2 = 9 is a rational number.
(iii) Given that z2 = 0.04
z2 = 0.04
z2 = 004/100
z = √(4/100)
z = 2/10
z = 1/5
It is a perfect square number.
Hence z2 = 0.04 is a rational number.
(iv) Given that u2 = 17/4
u2 = 17/4
u = √(17/4)
u = √17/2
Here √17 is an irrational number.
Hence u2 = 17/4 is also an irrational number.
(v) Given that v2 = 3
v = √3
we know that √3 = 1.732050807……..
Here √3 is an irrational number.
Hence v2 = 3 is also an irrational number.
(vi) w2 = 27
w = √(3×3 ×3)
w = 3√3
we know that √3 = 1.732050807……..
Here √3 is an irrational number.
Hence w2 = 27 is also an irrational number.
(vii) t2 = 0.4
t2 = 4/10
t = √(4/10)
t = 2/√10
we know that √10 = 3.162278……..
Here √10 is an irrational number.
Hence t2 = 0.4 is also an irrational number.
Question 6: Give two rational number lying between 0.232332333233332…. and 0.212112111211112....
Solution 6:
Let us assumed that a = 0.232332333233332…., b = 0.212112111211112....
Here the decimal representation of a and b are non-terminating and non-repeating. So we observe that in first decimal place of a and b have the same digit 2 but digit in the second place of their decimal representation are different.
Hence two rational numbers are 0.22222……… and 0.221…….lying between 0.232332333233332…. and 0.212112111211112.... .
Question 7: Give two rational number lying between 0.515115111511115…. and 0.5353353335…..... .
Solution 7:
Let us assumed that a = 0.515115111511115…., b = 0.535335333533335….....
Here the decimal representation of a and b are non-terminating and non-repeating. So we observe that in first decimal place of a and b have the same digit 5 but digit in the second place of their decimal representation are different.
Hence two rational numbers are 0.5152……… and 0.532…….lying between 0.515115111511115…. and 0.535335333533335.... .
Question 8: Find one irrational number between 0.2101 and 0.2222…… = 0.2.
Solution 8:
Let a = 0.2101 and b = 0.2222….. = 0.2
Here a and b are rational numbers. Since a has terminating number and b has non-terminating and repeating decimal numbers. We observe that in second decimal place a has 1 and b has 2.
Hence the required irrational number between 0.2101 and 0.2 is 0.2201001000100001……
Question 9: Find a rational number and also an irrational number lying between the numbers 0.3030030003…… and 0.3010010001……….. .Solution 9:
Let a = 0.3030030003….. and b = 0.3010010001……
Here decimal representation of a and b non-terminating and non-repeating. So a and b are irrational numbers. We observe that in first two decimals places of a and b have the same digit but the third placed decimal digit is different.
Hence the required rational number between 0.3030030003…… and 0.3010010001….. is 0.3011. And the required irrational number between 0.3030030003…… and 0.3010010001….. is 0.302002000200002……. .
Question 10: Find three different irrational number between the rational numbers 5/7 and 9/11 .
Solution 10:
Let us assumed that x = 5/7 and y = 9/11
We know that
5/7 = 0.714285 and 9/11 = 0.81
Here we observe that in the first decimal number x has start with 7 and second decimal number y has start with 8. So x < y. Now we can find a number which is non-terminating and non-recurring lying between them. We can find infinitely many such numbers. So the three irrational numbers are:
0.727227222722227………, 0.737337333733337……… and 0.747447444744447………
Question 11: Give an example of each, of two irrational number whose:
(i) Difference is a rational number.
(i) Difference is an irrational number.
(ii) Difference in an irrational number.
(iii) Sum in a rational number.
(iv) Sum is an irrational number.
(v) Product in a rational number.
(vi) Product in an irrational number.
(vii) Quotient in a rational number.
(viii) Quotient in an irrational number.
Solution 11:
(i) Let us assumed that our two irrational numbers are x = 2+√3 and y = √3
The difference of the irrational number is =
= (2 + √3) - √3
= 2+ √3 - √3
= 2
= 2 is a rational number. Hence it is prove that the difference of two irrational numbers can be rational number.
(ii) Let us assumed that our two irrational numbers are x = 2√3 and y = √3
The difference of the irrational number is =
= 2√3 - √3
= 2√3 - √3
= √3
= √3 is an irrational number. Hence it is prove that the difference of two irrational numbers can be irrational number.
(iii) Let us assumed that our two irrational numbers are x = √3 and y = -√3
The Sum of the irrational number is =
= √3 + (- √3)
= √3 - √3
= 0
= 0 is a rational number. Hence it is prove that the sum of two irrational numbers can be rational number.
(iv) Let us assumed that our two irrational numbers are x = 3√3 and y = 2√3
The Sum of the irrational number is =
= 3√3 + 2√3
= 5√3
= 5√3 is an irrational number. Hence it is prove that the sum of two irrational numbers can be irrational number.
(v) Let us assumed that our two irrational numbers are x = √2 and y = √8
The product of the irrational number is =
= √2 + √8
= √16
= 4
= 4 is a rational number. Hence it is proved that the product of two irrational numbers can be rational number.
(vi) Let us assumed that our two irrational numbers are x = √2 and y = √4
The product of the irrational number is =
= √2 + √4
= √8
= √8 is an irrational number. Hence it is proved that the product of two irrational numbers can be irrational number.
(vii) Let us assumed that our two irrational numbers are x = √8 and y = √2
The quotient of the irrational number is =
= √8/√2
= √(2 × 2 ×2)/√2
= (2√(2 ))/√2 (here √(2 ) × √(2 ) = 2)
= 2 is an irrational number. Hence it is proved that the quotient of two irrational numbers can be rational number.
(viii) Let us assumed that our two irrational numbers are x = √2 and y = √5
The quotient of the irrational number is =
= √2/√5
= √(2 )/√5 is an irrational number. Hence it is proved that the quotient of two irrational numbers can be irrrational number.
Question 12: Find two irrational numbers between 0.5 and 0.55 .
Solution 12:
Let a = 0.5 and b = 0.55
Here decimal representation of a and b terminating. So a and b are rational numbers. We observe that in first two decimals places of a and b have the same digit.
Hence the required irrational numbers between 0.5 and 0.55 are 0.510100100010000………. and 0.520200200020000………
Question 13: Find two irrational number lying between 0.1 and 0.12 .
Solution 13:
Let a = 0.1 and b = 0.12
Here decimal representation of a and b terminating. So a and b are rational numbers. We observe that in first two decimals places of a and b have the same digit.
Hence the required irrational numbers between 0.1 and 0.12 are 0.10100100010000………. and 0.110100100010000………
Question 14: Prove that √3+√5 is an irrational number.
Solution 14:
Let us assumed that x = √3+√5 is a rational number.
By squaring the both sides
x2 = (√3+√5)2
by using identity (x + y)2 = x2 + 2xy + y2
x2 = (√3+√5)2
x2 = (√3)2 + 2√3×√5 + (√5)2
x2 = 3 + 2√15 + 5
x2 = 8 + 2√15
x2 – 8 = 2√15
(x2-8)/2 = √15
As we assumed that x = √3+√5 is a rational number after solving this we get (x2-8)/2 = √15
In which (x2-8)/2 is rational number. But we know that √15 is an irrational number. Hence our assumption is wrong √3+√5 is an irrational number.
Exercise 1.5
Question 1: Complete the following sentences:
(i) Every point on the number line corresponds to a _________ number which many be either ___________ or __________.
(ii) The decimal form of an irrational number is neither __________ nor ___________.
(iii) The decimal representation of a rational number is either ___________ or ___________.
(iv) Every real number is either ___________ number or ___________ number.
Solution 1:
(i) Every point on the number line corresponds to a real number which many be either rational or irrational .
(ii) The decimal form of an irrational number is neither terminating nor repeating .
(iii) The decimal representation of a rational number is either terminating, non-terminating or recurring .
(iv) Every real number is either a rational number or an irrational number.
Question 2: Represent √6, √7, √8 on the number line.
Solution 2:
Representation of √6 on number line:-
Steps of making √6 on number line:-
For making √6 on line we have to make √5 on line first.
1. Draw a number line OF as shown in figure above.
2. Consider OB = 2cm and BC = 1cm. Now draw a right triangle OBC.
By Pythagoras theorem, we have
OC2 = OB2 + BC2
OC2 = (2)2 + (1)2
OC2 = 4 + 1
OC2 = 5
OC = √5
3. Take O as a centre put the needle of compass on O and measure line OC through compass.
4. Now, draw a circle with O and radius OC as shown in above figure.
5. We find that the circle cut the number line at point D.
6. Clearly, point D represent √5 on number line. OD = √5
7. By again Pythagoras theorem, we have
OE2 = OD2 + DE2
OE2 = (√5)2 + (1)2
OE2 = 5 + 1
OE2 = 6
OE = √6
8. Now, draw a circle with O and radius OE as shown in above figure.
9. We find that the circle cut the number line at point F.
10. Clearly, point F represent √6 on number line. OF = √6
(ii) Representation of √7 on number line:-
1. By Pythagoras theorem, we have
OG2 = OF2 + FG2
OG2 = (√6)2 + (1)2
OG2 = 6 + 1
OG2 = 7
OG = √7
2. First of all represent √6 on number line.
3. Now make right triangle from base OF = √6 cm and height FG =1cm
4. Draw a circle with O and radius OG as shown in above figure.
5. We find that the circle cut the number line at point H. As shown in above figure.
4. Clearly, point H represent √7 on number line. OH = √7.
(iii) Representation of √8 on number line:-
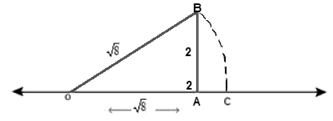
1. By Pythagoras theorem, we have
OB2 = OA2 + AB2
OG2 = (2)2 + (2)2
OG2 = 4 + 4
OG2 = 8
OG = √8
2. Now make right triangle from base OA = 2 cm and height AB =2cm
4. Draw a circle with O and radius OB as shown in above figure.
5. We find that the circle cut the number line at point C. As shown in above figure.
4. Clearly, point C represent √8 on number line. OC = √8.
Question 3: Represent√3.5, √9.4, √10.5 on the real number line.
Solution 3:
(i) Representation of √(3.5) on number line:-
1. Draw a number line and mark point A and B on it. The length of AB = 3.5 cm as shown in figure above.
2. Increase the line AB about 1 cm and make point C on it.
3. Find mid-point of AC. Let the mid-point be O.
AC = AB + BC
AC = 3.5cm + 1cm
AC = 4.5cm
So the mid-point of AC = 4.5/2 = 2.25cm
OA = OC
4. Draw a circle taking O as a centre and OA as radius draw a semi-circle. Also draw a line passing through B perpendicular to OB. Suppose it cuts the semi-circle at D. Consider triangle OBD; it is right angled at B.
BD2 = OD2 – OB2
BD2 = OD2 – (OC – BC)2
BD2 = OD2 – (OC – BC)2
BD2 = OD2 – {(OC)2 – 2(OC)(BC) + (BC)2}
BD2 = OD2 – OC2 + 2(OC)(BC) – BC2 [we know that OC = OD]
BD2 = 2(OC)(BC) – BC2
BD2 = 2(2.25)(1) – (1)2
BD = √(4.50-1 )
BD = √(3.50 )
5. Draw a circle by taking B as the centre and BD as radius and produce point E. We observe that circle also cut number line at point E.
6. Clearly, point E represent √3.5 on number line. OE = √3.5.
(ii) Representation of √(9.4) on number line:-
1. Draw a number line and mark point A and B on it. The length of AB = 9.5 cm as shown in figure above.
2. Increase the line AB about 1 cm and make point C on it.
3. Find mid-point of AC. Let the mid-point be O.
AC= AB + BC
AC =9.4cm + 1cm
AC = 10.4cm
So the mid-point of AC = 10.4/2 = 5.2cm
OA = OC
4. Draw a circle taking O as a centre and OA as radius draw a semi-circle. Also draw a line passing through B perpendicular to OB. Suppose it cuts the semi-circle at D. Consider triangle OBD; it is right angled at B.
BD2 = OD2 – OB2
BD2 = OD2 – (OC – BC)2
BD2 = OD2 – (OC – BC)2
BD2 = OD2 – {(OC)2 – 2(OC)(BC) + (BC)2}
BD2 = OD2 – OC2 + 2(OC)(BC) – BC2 [we know that OC = OD]
BD2 = 2(OC)(BC) – BC2
BD2 = 2(5.2)(1) – (1)2
BD = √(10.40-1 )
BD = √(9.40 )
5. Draw a circle by taking B as the centre and BD as radius and produce point E. We observe that circle also cut number line at point E.
6. Clearly, point E represent √9.4 on number line. OE = √9.4.
(iii) Representation of √(10.5) on number line:-
1. Draw a number line and mark point A and B on it. The length of AB = 9.5 cm as shown in figure above.
2. Increase the line AB about 1 cm and make point C on it.
3. Find mid-point of AC. Let the mid-point be O.
AC= AB + BC
AC =10.5cm + 1cm
AC = 11.5cm
So the mid-point of AC = 11.5/2 = 5.75cm
OA = OC
4. Draw a circle taking O as a centre and OA as radius draw a semi-circle. Also draw a line passing through B perpendicular to OB. Suppose it cuts the semi-circle at D. Consider triangle OBD; it is right angled at B.
BD2 = OD2 – OB2
BD2 = OD2 – (OC – BC)2
BD2 = OD2 – (OC – BC)2
BD2 = OD2 – {(OC)2 – 2(OC)(BC) + (BC)2}
BD2 = OD2 – OC2 + 2(OC)(BC) – BC2 [we know that OC = OD]
BD2 = 2(OC)(BC) – BC2
BD2 = 2(5.75)(1) – (1)2
BD = √(11.50-1 )
BD = √(10.50 )
5. Draw a circle by taking B as the centre and BD as radius and produce point E. We observe that circle also cut number line at point E.
6. Clearly, point E represent √10.50 on number line. OE = √10.50 .
Question 4: Find whether the following statements are true or false.
(i) Every real number is either rational or irrational.
(ii) π is an irrational number.
(iii) Irrational numbers cannot be represented by point on the number line.
Solution 4:
(i) True, Rational and irrational number are taken together from the family of real numbers. So every real number is either rational or irrational number.
(ii) True, As we know that every irrational numbers are non-terminating and non-recurring. The value of π = 3.141………. so it is irrational number.
(iii) False, Irrational number can be represented by point on the number line.
Exercise 1.6
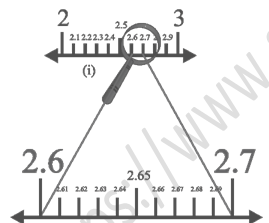
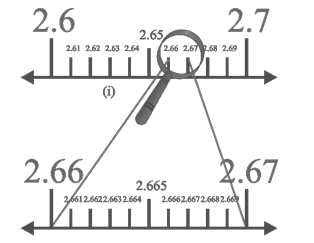
Question 1: Visualise 2.665 on the number line, using successive magnification.
Solution 1:
Representation of 2.665 on number line:-
1. We know that 2.665 lie between 2 and 3.
2. Now we divide this into 10 equal parts and mark each point as shown in figure. Ex. 2.1, 2.2, 2.3……..2.9.
3. Now, 2.665 lies between 2.6 and 2.7 so let us focus on the portion between 2.6 and 2.7.
4. We divide it again in 10 equal part and mark each point as shown in figure. Ex. 2.61, 2.62………2.69.
5. Now, 2.665 lies between 2.66 and 2.67 so let us focus on the portion between 2.66 and 2.67.
6. We divide it again in 10 equal part and mark each point as shown in figure. Ex. 2.661, 2.662………2.669.
7. The first mark represents 2.661 the next one represents 2.662, and so on. So, 2.665 is the 5th mark in these subdivisions.
Question 2: Visualise the representation of 5.37̅ on the number line upto 5 decimal places, that is upto 5.37777.
Solution 2:
Representation of 5.37777 on number line:-
1. We know that 5.37777 lie between 5 and 6.
2. Now we divide this into 10 equal parts and mark each point as shown in figure. Ex. 5.1, 5.2, 5.3……..5.9.
3. Now, 5.37777 lies between 5.3 and 5.4 so let us focus on the portion between 5.3 and 5.4.
4. We divide it again in 10 equal parts and mark each point as shown in figure. Ex. 5.31, 5.32………5.39.
5. Now, 5.3777 lies between 5.37 and 5.38 so let us focus on the portion between 5.37 and 5.38.
6. We divide it again in 10 equal parts and mark each point as shown in figure. Ex. 5.371, 5.372………5.379.
7. The first mark represents 5.371 the next one represents 5.372, and so on. So, 5.377 is the 7th mark in these subdivisions. Notice that 5.37 is located closer to 5.3778 than to 5.3777 as shown in figure.

