Question :8. The diameter of a wheel of a car is 63 cm. Find the distance travelled by the car during the period, the wheel makes 1000 revolutions.
Solution 8:
It should be remembered that the cycle travels a distance equal to the diameter of the wheel in one revolution.
According to question the diameter of the wheel = 63 cm
Formula of circumference of the wheel = π d
Value of π = (22/7)
=22/7 x 63
= 198 cm.
Thus, the cycle covers 198 cm in one revolution.
Thus, the distance covered by the cycle in 1000 revolutions = 198 x 1000
= 198000 cm
= 1980 m.
Question :9. The diameter of a wheel of a car is 98 cm. How many revolutions will it make to travel 6160 meters.
Solution 9:
The automobile travels a distance equal to the diameter of the wheel in one revolution.
According to question diameter of the wheel of a car = 98 cm
Circumference of the wheel of the car = π d
Value of π = (22/7)
= 22/7 x 98
= 308 cm
The distance travelled by the car in one revolution = 308 cm
Total distance travelled by the car = 6160 m = 616000 cm
Thus, number of revolutions = (total distance travelled by the car)/(distance travelled by the car in one revolution)
Number of revolutions = 616000/308 = 2000
Question :10. The moon is about 384400 km from the earth and its path around the earth is nearly circular. Find the circumference of the path described by the moon in lunar month.
Solution 10:
According to the question it is given that, the radius of the path described by the moon around the earth = 384400 km
The circumference of the path,
C = 2 π r
Value of π = (22/7)
C = 2 × 22/7 × 384400
C = 2416228.57 km
Question :11. How long will John take to make a round of a circular field of radius 21 m cycling at the speed of 8 km/hr.?
Solution 11:
According to the question the radius of the circular field = 21 m
Circumference of the circular field = 2 π r
Value of π = (22/7)
C = 2 × 22/7 × 21
= 132 m
If John cycles at a speed of 8 km/hr
Convert km into m
So, John covers 8000 m in 1 hour.
So, time needed to cover 132 m
= 132/8000
= 0.0165 hours
As, 1 hour = 3600 seconds
Convert hours into seconds
0.0615 hours = 0.0165 x 3600
= 59.4 seconds.
Question :12. The hour and minute hands of a clock are 4 cm and 6 cm long respectively. Find the sum of the distances travelled by their tips in 2 days.
Solution 12:
Length of the hour hand is 4 cm, the radius of the path inscribed by the hour hand.
Length of the minute hand is 6 cm, the radius of the path inscribed by the minute hand.
For hour hand the circumference of the path inscribed by = 2 π r
Value of π = (22/7)
C = 2 × 22/7 × 4
= 176/7 cm
The hour hand makes 2 revolutions in one day.
Thus, distance covered by the hour hand in 2 days
= 176/7 × 2 × 2
= 100.57 cm
The distance covered by the minute hand in 1 revolution = 2 π r
C = 2 × 22/7 × 6
= 264/7
The minute hand makes 1 revolution in one hour.
In 1 day, it makes 24 revolutions.
In 2 days, it makes 2 × 24 revolutions.
The distance covered by the minute hand in 2 days
= 2 × 24 × 264/7
= 12672/7
= 1810.28 cm
By the hour and minute hands the sum of the distances travelled in 2 days = 1810.28 + 100.57
= 1910.85 cm
Question :13. A rhombus has the same perimeter as the circumference of the circle. If the side of the rhombus is 2.2m, find the radius of the circle.
Solution 13:
The side of a rhombus = 2.2 m
Formula of the perimeter of the rhombus = 4 x side
= 4 x 2.2 m
= 8.8 m.
According to the question,
Perimeter of the rhombus = Circumference of the circle
8.8 = 2 π r
Value of π = (22/7)
8.8 = 2 × 22/7 × r
r = ((8.8 × 7))/44
r = 61,6/44
r = 1.4 m
Thus, radius of the circle = 1.4m
Question :14. A wire is looped in the form of a circle of radius 28 cm. It is re-bent into a square form. Determine the length of the side of the square.
Solution 14:
The radius of the circle = 28 cm
Formula of circumference of the circle = 2 π r
Value of π = (22/7)
C = 2 × 22/7 × 28
C = 176 cm
Let x cm be the side of the square.
Then, circumference of the circle = the perimeter of the square
Perimeter of square = 4x
176 = 4 × x
x = 176/4
= 44
Thus, the side of the square = 44 cm
Question :15. A bicycle wheel makes 5000 revolutions in moving 11 km. Find the diameter of the wheel.
Solution 15:
Total distance covered by bicycle in 5000 revolutions = 11 km = 11000 m
Thus, distance covered in one revolution = 11000/5000 = 2.2 m = 11/5
Distance covered in one revolution = Circumference of the wheel
C = π d Value of π = (22/7)
11/5 = 22/7 d
d = ((11 × 7))/((5 × 22))
= 77/110
d = 0.7 m
Thus, diameter of wheel = 0.7 m = 70 cm
Question :16. A boy is cycling such that the wheels of the cycle are making 140 revolutions per minute. If the diameter of the wheel is 60 cm, calculate the speed per hour with which the boy is cycling.
Solution 16:
The diameter of the wheel = 60 cm
The wheel covered distance in 1 revolution = Circumference of the wheel
Circumference of the wheel= π d
Where, π = (22/7)
= 22/7 × 60 cm
The wheel covered distance in 140 revolutions = 22/7 × 60 × 140
= 26400 cm
Thus, the wheel covers 26400 cm in 1 minute.
Then, speed = 26400/100 × 60 m/hr
= 264 × 60 m/hr.
= (264 × 60)/1000 km/hr.
= 15.84 km/hr.
The speed with which the boy is cycling is 15.84 km/hr.
Question :17. The diameter of the driving wheel of a bus is 140 cm. How many revolutions per minute must the wheel make in order to keep a speed of 66 km per hour?
Solution 17:
Wheels’ diameter = 140 cm
Desired speed of the bus = 66 km/hr.
The wheel covered distance in 1 revolution = Circumference of the wheel
Circumference of the wheel = π d
Where, π = (22/7)
C = 22/7 × 140
C = 440 cm
Now, the desired speed of the bus = 66 km/hr.
= (66 × 1000 × 100)/60 = 110000 cm/min
Revolutions per minute = 110000/440
= 250
To maintain a speed of 66 km/hr., the bus must turn 250 times per minute.
Question :18. A water sprinkler in a lawn sprays water as far as 7 m in all directions. Find the length of the outer edge of wet grass.
Solution 18:
A water sprinkler in a lawn sprays water at a distance of 7 m in all directions, according to the question.
As a result, the wet area appears in a circular region with a radius of 7 meters.
The length of the outer edge of the wet grass = Circumference of circle
Circumference of the circle = 2 π r
Where, π = (22/7)
C = 2 × 22/7 × 7
C = 44 m
Question :19. A well of diameter 150 cm has a stone parapet around it. If the length of the outer edge of the parapet is 660 cm. then find the width of the parapet.
Solution 19:
The wells’ Diameter = 150 cm
Length of the outer edge of the parapet = 660 cm
Now we have to find width of the parapet
Now, radius of well = half of diameter = 150/2 = 75 cm
Assume that the stone parapet is x cm wide. According to the issue, the parapet's outer edge forms a circular region with a radius of (x + 75) cm.
So, 660 = 2 × 22/7 × (x + 75)
((660 × 7))/((2 × 22)) = x + 75
4620/44 = x + 75
105 = x + 75
x = 105 – 75
x = 30
The parapets’ width is = x = 30cm
Question :20. An ox in a kolhu (an oil processing apparatus) is tethered to a rope 3 m long. How much distance does it cover in 14 rounds?
Solution 20:
Radius of the circular path traced by the ox = 3 m and
Distance covered by an ox in 1 round = Circumference of the circular path
Circumference = 2 π r
Where, π = (22/7)
C = 2 × 22/7 × 3 m
Distance covered in 14 rounds = 2 × 22/7 × 3 × 14C = 264 m
Exercise 21.2
Question :1. Find the area of a circle whose radius is
(i) 7 cm
(ii) 2.1 m
(iii) 7 km
Solution 1:
(i) Radius = 7 cm
Formula of area of circle = π r2
A = 22/7 × 72
A = 22 × 7
A = 154 cm2
(ii) Radius = 2.1 m
Formula of area of circle = π r2
A = 22/7 × (2.1)2
A = 22/7 × 4.41
A = 13.86 m2
(iii) Radius = 7 km
Formula of area of circle = π r2
A = 22/7 × 72
A = 22 × 7
A = 154 km2
Question :2. Find the area of a circle whose diameter is
(i) 8.4 cm
(ii) 5.6 m
(iii) 7 km
Solution 2:
(i) Diameter = 8.4 cm
Thus, the radius, r = d/2 = 8.4/2 = 4.2
Formula of area of circle = π r2
A = 22/7 × (4.2)2
A = 55.44 cm2
(ii) Diameter = 5.6 cm
Thus, the radius, r = d/2 = 5.6/2 = 2.8
Formula of area of circle = π r2
A = 22/7 × (2.8)2
A = 24.64 cm2
(iii) Diameter = 7 km
Thus, the radius, r = d/2 = 7/2 = 3.5
Formula of area of circle = π r2
A = 22/7 × (3.5)2
A = 38.5 km2
Question :3. The area of a circle is 154 cm2. Find the radius of the circle.
Solution 3:
Area of the circle = 154 cm2
Formula of area of circle = π r2
154 = 22/7r2
r2 = ((154 × 7))/22
r2 = 49
r = 7 cm
Question :4. Find the radius of a circle, if its area is
(i) 4 π cm2
(ii) 55.44 m2
(iii) 1.54 km2
Solution 4:
(i) Area = 4 π cm2
Formula of the area of circle = π r2
A = π r2
4 π = π r2
r2 = 4
Thus, r = 2 cm
(ii) Area = 55.44 cm2
Formula of area of circle = π r2
55.44 = π r2
r2 = ((55.44 × 7))/22
r2 = 17.64 m
r = 4.2 m
(iii) Area = 1.54 km2
Formula of area of circle = π r2
A = π r2
1.54 = π r2
r2 = ((1.54 × 7))/22
r2 = 0.49 km
r = 0.7 km
r = 700m
Question :5. The circumference of a circle is 3.14 m, find its area.
Solution 5:
Given circumference = 3.14m
We know that circumference of circle = 2 π r
3.14 = 2 × 3.14 × r
r = 3.14/((2 × 3.14))
r = 0.5
We know that area of circle = π r2
A = 22/7 × (0.5)2
A = 0.785 m2
Question :6. If the area of a circle is 50.24 m2, find its circumference.
Solution 6:
Area of a circle is 50.24 m2
Formula of the area of circle = π r2
50.24 = 22/7 × r2
r2 = ((50.24 × 7))/22
r2 = 15.985
r = 3.998 m
the circumference of circle = 2 π r
C = 2 × 22/7 × 3.998
C = 25.12 m
Question :7. A horse is tied to a pole with 28 m long string. Find the area where the horse can graze. (Take π = 22/7).
Solution 7:
The length of the string = 28m
The distance that the horse will graze is equal to the area of a circle with a circumference of 28 m.
So, the area = π r2
A = 22/7 × (28)2
A = 2464 m2
Question :8. A steel wire when bent in the form of a square encloses an area of 121 cm2. If the same wire is bent in the form of a circle, find the area of the circle.
Solution 8:
Area of the square = 121 cm2
(Side)2 = 121
Thus side = 11 cm
The perimeter of the square = 4 (side)
= 4 (11)
= 44 cm
According to the question circumference of the circle = perimeter of the square
So let r be the radius of the circle
2 π r = 44
2 × 22/7 × r = 44
Thus, the r = 7 cm
Area of the circle = π r2
A = 22/7 × (7)2
A = 154 cm2
Question :9. A road which is 7 m wide surrounds a circular park whose circumference is 352 m. Find the area of road.
Solution 9:
Circumference of park = 352 m
But we know that circumference of circle = 2 π r = 352 m
2 × 22/7 × r = 352
r = ((352 × 7))/44
r = 56 m
Radius of the path with the 7m wide road = (r + 7) = 56 + 7 = 63m
Thus, area of the road = π × (63)2 – π × (56)2
A = 22/7 × 63 × 63 – 22/7 × 56 × 56
A = 22 (9 × 63 – 8 × 56)
A = 22 (567 – 448)
A = 2618 m2
Question :10. Prove that the area of a circular path of uniform width h surrounding a circular region of radius r is πh (2r + h).
Solution 10:
Let radius of circular region = r
The radius of a circular path with a uniform width h that surrounds the circular area of radius,
r = r + h
Thus, area of path = π (r + h)2 – πr2
= π r2 + π h2 + 2 π r h – π r2
= π h (2r + h)
So, the proof.
Question :11. The perimeter of a circle is 4πr cm. What is the area of the circle?
Solution 11:
Perimeter of circle = 4πr cm
Can be written as = 2 π (2r)
Formula of the perimeter of a circle = 2 π r
Thus, radius = 2r
We also know that area of circle = π r2
= π (2r)2
= 4 π r2 cm2
Question :12. A wire of 5024 m length is in the form of a square. It is cut and made a circle. Find the ratio of the area of the square to that of the circle.
Solution 12:
According to the question, Perimeter of the square = 5024 m
⇒ 4 × side = 5024
⇒ Side = 5024/4
⇒ Side = 1256 m
If the same wire converted into the other of a circle.
Thus, Circumference of the circle = Perimeter of the square
⇒ 2πr = 5024
⇒ 2 × π × r = 5024
⇒ r = 2512/π
We know that area of the square: Area of the circle = (side)2 : πr2
(Area of square)/(area of circle) = (side)2/ πr2
(Area of square)/(area of circle) = ((1256 × 1256))/((π × 2512/π ×2512/π) )
= ((1256 × 1256 × 22))/((2512 × 2512 × 7))
= 11/14
Area of the square: Area of the circle = 11: 14
Question :13. The radius of a circle is 14 cm. Find the radius of the circle whose area is double of the area of the circle.
Solution 13:
Let be A1 is the area of the circle whose radius is 14 cm.
Formula of the area of the circle = πr2
Thus, A1 = π (14)2
Let A2 and r2 be the area and radius of the second circle respectively whose area is double the area of circle A1.
A2 = 2 A1
⇒ π (r2)2 = 2 × π (14)2
⇒ (r2)2 = 2 × (14)2
⇒ r2 = 14√2 cm
So, the radius of the circle A2 is 14√2 cm.
Question :14. The radius of one circular field is 20 m and that of another is 48 m. find the radius of the third circular field whose area is equal to the sum of the areas of two fields.
Solution 14:
In the given information, Let A1 = the area of the circle whose radius is 20 m
A2 = the area of the circle whose radius is 48 m
Now we must determine the radius of the third circle whose area equals the number of the areas of the two fields.
So,
A3 = A1 + A2
⇒ π r2 = π (20)2 + π (48)2
⇒ π r2 = π [(20)2 + (48)2]
⇒ r2 = 400 + 2304
⇒ r = 52 m
Thus, radius = 52 m
Question :15. The radius of one circular field is 5 m and that of the other is 13 m. Find the radius of the circular field whose area is the difference of the areas of first and second field.
Solution 15:
In the given information, let A1 = the area of the circular field whose radius is 5 m
A2 = the area of the circular field whose radius is 13 m
Now we must calculate the area of a circular field whose area equals the sum of the first and second fields' regions.
A3 = A2 – A1
⇒ π r2 = π (13)2 – π (5)2
⇒ π r2 = π [(13)2 – (5)2]
⇒ r2 = 169 – 25
⇒ r2 = 144
⇒ r = 12 m
So, the radius of the circular field is 12 m.
Question :16. Two circles are drawn inside a big circle with diameters 2/3rd and 1/3rd of the diameter of the big circle as shown in Fig. 18. Find the area of the shaded portion, if the length of the diameter of the circle is 18 cm.
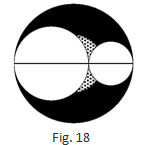
Solution 16:
According to the question, diameter of the big circle = 18 cm
Radius of the big circle = 9 cm
Area of the big circle, A = π r2 = π (9)2 = 81π cm2
Let d1 = 2/3× 18 = 12 cm
r1 = 6 cm
Area of the circle, A1 = π r2 = π (6)2 = 36π cm2
d2 = 1/3 × 18 = 6 cm
r2 = 3 cm
Area of the circle, A2 = π r2 = π (3)2 = 9π cm2
Area of the shaded portion = A – (A1 + A2)
Area of the shaded portion = 81π – (36π + 9π) = 36π cm2
Question :17. In Fig. 19, the radius of quarter circular plot taken is 2 m and radius of the flower bed is 2 m. Find the area of the remaining field.
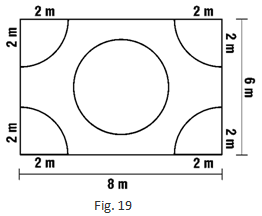
Solution 17:
Radius of flower bed = 2 m
Area of flower bed = π r2 = π (2)2 = 4π
Radius of the quarter circular plot = 2 m
Area of the quarter circular plot = (π r2)/4
Area of 4 quarter circular plots = 4 × (π r2)/4
= π r2
= π (2)2
= 4π
Formula of the area of the rectangular region = Length x Breadth
Area of the rectangular region = 8 x 6 = 48 m2
Area of the remaining field = Area of the rectangular region – (Area of 4 quarter circular plots + Area of the flower bed)
Area of the remaining field = 48 – (4π + 4π)
= 48 – 25.12
= 22.88 m2
Question :18. Four equal circles, each of radius 5 cm, touch each other as shown in Fig. 20. Find the area included between them. (Take π = 3.14).
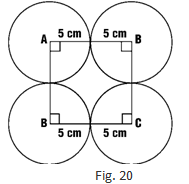
Solution 18:
According to the diagram, side of the square = 10 cm
Formula of area of the square = side x side
= 10 x 10 = 100 cm2
Radius of the quarter circle = 5 cm
Area of the quarter circle = (π r2)/4
Area of 4 quarter circle = 4 × (π r2)/4
= π r2
= 3.14 × (5)2
= 78.5 cm2
Area included in the quarter circle = Area of the square – Area of the four quarter circles
Area included in them = (100 – 78.5) cm2
= 21.5 cm2
Question :19. The area of circle is 100 times the area of another circle. What is the ratio of their circumferences?
Solution 19:
Let be A1 and A2 the area of the circles and their circumference be c1 and c2 respectively.
According to the question, A1 = 100 A2
⇒ π (r1)2 = 100 × π (r2)2
⇒ r1 = 10 r2
⇒ r1/r2 = 10/1 -(i)
After finding the ratios of the circumference;
C1: C2 = 2πr1: 2πr2
C1/C2 = (2πr1)/ (2πr2)
C1/C2 = r1/r2
Putting the value of r1/r2 from equation (i)
C1/C2 = 10/1
C1: C2 = 10/1
So, the ratio of their circumferences is 10: 1.

