Step 1. Make a line PQ.
Step 2. Select any two points A and B on the line PQ.
Step 3. Construct ∠PBF = 90o and ∠QAE = 90o
Step 4. Use point A as center and radius 5 cm cut AE at C.
Step 5. Use point B as center and radius 5 cm cut BF at D.
Step 6. Connect CD and make the appropriate line parallel to AB and at a distance of 5 cm from it on either side.
Question :3. Draw an equilateral triangle one of whose sides is of length 7 cm.
Solution 3:
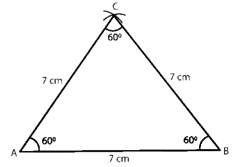
Construction:
Step 1. Make a line segment AB with length 7 cm.
Step 2. Use center point A, make an arc of radius 7 cm.
Step 3. Use center point B, make an arc of radius 7 cm intersecting the previously drawn arc at C.
Step 4. Connect AC and BC to get the required triangle.
Question :4. Draw a triangle whose sides are of lengths 4 cm, 5 cm and 7 cm. Draw the perpendicular bisector of the largest side.
Solution 4:
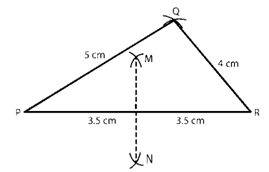
Construction:
Step 1. Make a 7-cm-long line segment PR.
Step 2. Make a 5 cm radius arc with center P.
Step 3. Make an arc of radius 4 cm with center R intersecting the previously drawn arc at Q.
Step 4. To make the appropriate triangle, connect PQ and QR.
Step 5. On either side of P, Make arcs with a radius greater than half of PR.
Step 6. Make arcs from R on both sides of PR, intersecting the arcs drawn in the previous step at M and N, with the same radius as in the previous step.
Step 7. MN is the perpendicular bisector of the largest side that is needed.
Question :5. Draw a triangle ABC with AB = 6 cm, BC = 7 cm and CA = 8 cm. Using ruler and compass alone, draw (i) the bisector AD of ∠A and (ii) perpendicular AL from A on BC. Measure LAD.
Solution 5:
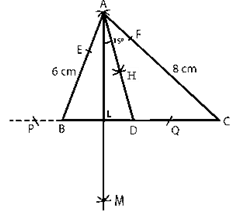
Construction:
Step 1. Make a 7-cm-long line segment BC.
Step 2. Make a 6 cm radius arc with center B.
Step 3. Make an arc of radius 8 cm with center C intersecting the previously drawn arc at A.
Step 4. To make the requisite triangle, connect AC and AB.
Angle bisector steps:
Step 5. Cut equal-radius arcs from A, intersecting AB and AC at E and F, respectively.
Step 6. Cut arcs of equal radius from E and F, intersecting at point H.
Step 7. Connect AH and extend it to form the angle bisector of angle A, which intersects line BC at D.
Step 8. Steps perpendicular to the line BC from Point A.
Step 9. Cut arcs of equal radius from A that intersect BC at P and Q, respectively (Extend BC to Make these arcs).
Step 10. Cut arcs of equal radius from P and Q, intersecting at M.
Step 11. Cut BC at L with AM.
Step 12. The line BC is perpendicular to AL.
Step 13. LAD has a 15o angle.
Question :6. Draw △DEF such that DE= DF= 4 cm and EF = 6 cm. Measure ∠E and ∠F.
Solution 6:
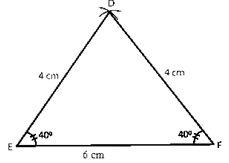
Construction:
Step 1. Make a 6 cm long EF line segment.
Step 2. Make an arc with a radius of 4 cm with E as the middle.
Step 3. Make an arc of radius 4 cm with F as the origin, intersecting the previous arc at D.
Step 4. Link DE and DF to form the DEF triangle.
Step 5. We get ∠E= ∠F= 40o by measuring.
Question :7. Draw any triangle ABC. Bisect side AB at D. Through D, draw a line parallel to BC, meeting AC in E. Measure AE and EC.
Solution 7:
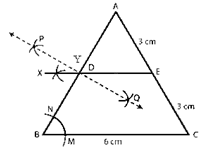
Firstly, Make a triangle, Name then ABC with each side = 6 cm.
Construction to bisect line AB:
Step 1. On either side of line AB, Make an arc from A.
Step 2. Make an arc from B on either side of AB, intersecting the arcs drawn in the previous step at P and Q, with the same radius as in the previous step.
Step 3. Connect PQ at D, cutting AB. The perpendicular bisector of AB is PQ.
Parallel line to BC:
Step 4. Make an arc with B as the base, cutting BC and BA at M and N, respectively.
Step 5. Make an arc on the opposite side of AB to cut AB at Y using center D and the same radius as in the previous step.
Step 6. With a radius of MN and a center of Y, Make an arc that intersects the arc drawn in the previous phase at X.
Step 7. Connect XD and extend it to E, where it intersects AC.
Step 8. The requisite parallel line is DE.
Exercise 17.3
Question :1. Draw △ABC in which AB = 3 cm, BC = 5 cm and ∠B = 70o.
Solution 1:
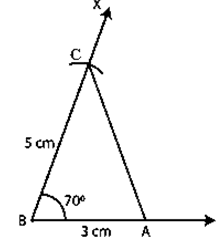
Construction:
Step 1. Make a 3 cm long line segment AB.
Step 2. Make the angle ∠XBA=70o.
Step 3. At C, cut an arc on BX at a 5 cm radius.
Step 4. Connect AC to complete the triangle.
Question :2. Draw △ABC in which ∠A=70o. AB = 4 cm and AC= 6 cm. Measure BC.
Solution 2:
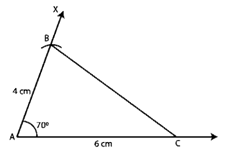
Construction:
Step 1. Make a 6 cm long line segment AC.
Step 2. Make an angle ∠XAC=70o.
Step 3. At B, Make an arc on AX at a distance of 4 cm.
Step 4. Connect BC to form the triangle you want.
Step 5. We can see that BC is equal to 6 cm.
Question :3. Draw an isosceles triangle in which each of the equal sides is of length 3 cm and the angle between them is 45o.
Solution 3:
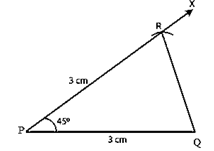
Construction:
Step 1. Make a 3 cm long PQ line segment.
Step 2. Make a ∠QPX=45o drawing.
Step 3. On PX, cut an arc at R at a distance of 3 cm.
Step 4. Connect QR to get the triangle.
Question :4. Draw △ABC in which ∠A = 120o, AB = AC = 3 cm. Measure ∠B and ∠C.
Solution 4:
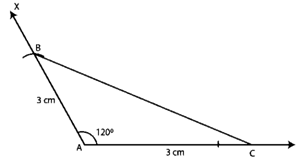
Construction:
Step 1. Make a 3 cm long line segment AC.
Step 2. Make the angle ∠XAC = 120o.
Step 3. At B, Make an arc on AX at a distance of 3 cm.
Step 4. Connect BC to complete the triangle.
Step 5. We get ∠B = ∠C = 30o by measuring.
Question :5. Draw △ABC in which ∠C = 90o and AC = BC = 4 cm.
Solution 5:
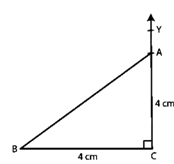
Construction:
Step 1. Make a 4 cm long line segment BC.
Step 2. Make ∠BCY=90° at C.
Step 3. At A, Make an arc on CY at a distance of 4 cm.
Step 4. connect AB, ABC is the required triangle.
Question :6. Draw a triangle ABC in which BC = 4 cm, AB = 3 cm and ∠B = 45o. Also, draw a perpendicular from A on BC.
Solution 6:
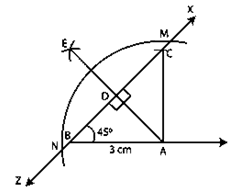
Construction:
Step 1. Make a 3 cm long line segment AB.
Step 2. At C, Make a 45o angle and cut an arc with a radius of 4 cm at this angle.
Step 3. Connect AC to complete the triangle.
Step 4. Make intersecting arcs at M and N with A as the middle.
Step 5. Cut an arc on the opposite side of A with a middle M and a radius greater than half of MN.
Step 6. Cut an arc intersecting the previous arc at E with N as the center and the same radius as in the previous stage.
Step 7. Connect AE at D, where it meets BC, and AE becomes the appropriate perpendicular.
Question :7. Draw a triangle ABC with AB = 3 cm, BC = 4 cm and ∠B = 60o. Also, draw the bisector of angles C and A of the triangle, meeting in a point O. Measure ∠COA.
Solution 7:
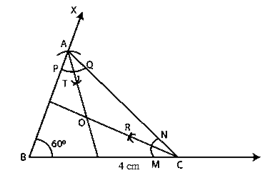
Construction:
Step 1. Make a BC = 4 cm line segment.
Step 2. Make an angle ∠CBX = 60o.
Step 3. Make a 3 cm radius arc on BX, cutting BX at A.
Step 4. Connect AC to complete the triangle.
Angle bisector for angle A:
Step 5. Cut arcs of the same radius with A as the middle, cutting AB and AC at P and Q, respectively.
Step 6. Cut arcs of the same radius from P and Q, intersecting at T.
Step 7. Combine AT and A to get the angle bisector of A.
Angle bisector for angle C:
Step 8.Cut arcs of the same radius with A as the middle, cutting CB and CA at M and N, respectively.
Step 9. Cut arcs of the same radius intersecting at R from M and N.
Step 10. To get the angle bisector of angle C, connect CR.
Step 11. Make an O at the intersection of CR and AT.
Step 12. Angle ∠COA = 120o.
Exercise 17.4
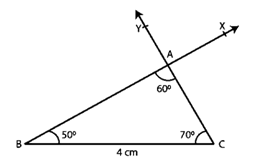
Question :1. Construct ∆ABC in which BC = 4 cm, ∠B = 50o and ∠C = 70o.
Solution 1:
Construction:
Step 1. Make a 4 cm long line segment BC.
Step 2. Make ∠CBX, so that it equals ∠CBX=50o.
Step 3. Make ∠BCY =70o by placing Y on the same side of BC as X.
Step 4. Assume that CY and BX cross at A.
Step 5. The requisite triangle is ABC.
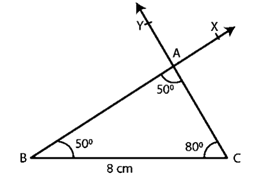
Question :2. Draw ∆ABC in which BC = 8 cm, ∠B = 50o and ∠A = 50o.
Solution 2:
Construction:
Step 1. Make an 8-cm-long line segment BC.
Step 2. Make ∠CBX so that it equals ∠CBX = 50o.
Step 3. Make ∠BCY so that ∠BCY = 80o, with Y on the same side of BC as X.
Step 4. Assume that CY and BX cross at A.
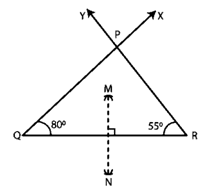
Question :3. Draw ∆ABC in which ∠Q = 80o, ∠R = 55o and QR = 4.5 cm. Draw the perpendicular bisector of side QR.
Solution 3:
Construction:
Step 1. Make a QR = 4.5 cm line section.
Step 2. Make ∠RQX = 80° and ∠QRY = 55o.
Step 3. Assume that QX and RY intersect at P, forming the appropriate triangle PQR.
Step 4. Make arcs on both sides of QR with Q as the middle and a radius greater than 4.5 cm.
Step 5. Make arcs intersecting the previous arcs at M and N with R as the middle and a radius greater than 4.5 cm.
Step 6. Connect MN.
Step 7. MN is the perpendicular bisector of QR that is necessary.
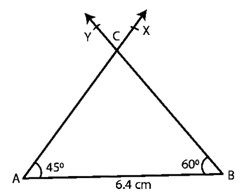
Question :4. Construct ∆ABC in which AB = 6.4 cm, ∠A = 45o and ∠B = 60o
Solution 4:
Construction:
Step 1. Make a line segment with the length AB = 6.4 cm.
Step 2. Make ∠BAX = 45o angle.
Step 3. ∠ABY should be drawn with Y on the same side of AB as X, so that ∠ABY = 60o.
Step 4. Assume the AX and BY cross at C.
Step 5. The requisite triangle is ABC.
Question :5. Draw ∆ABC in which AC = 6 cm, ∠A = 90o and ∠B = 60o
Solution 5:
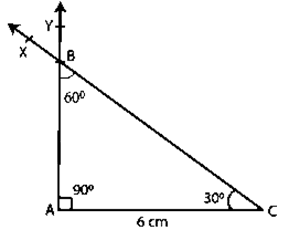
Construction:
Step 1. Make a line segment with the length AC = 6 cm.
Step 2. Make ∠ACX = 30o angle.
Step 3. Make ∠CAY so that Y is on the same side of AC as X and ∠CAY = 90o.
Step 4. Team up with CX and AY. Allow these to cross at B.
Step 5. The required triangle is ABC, with an angle of ∠ABC = 60o.
Exercise 17.5
Question :1. Draw a right triangle with hypotenuse of length 5 cm and one side of length 4 cm.
Solution 1:
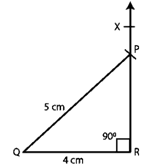
Construction:
Step 1. Make a QR = 4 cm line section.
Step 2. Make an angle 90o ∠QRX.
Step 3. Make an arc of the triangle with a middle Q and a radius PQ = 5 cm to intersect ray RX at P.
Step 4. Combine PQ and PQR to form the ideal triangle PQR.
Step 5. The required triangle is PQR.
Question :2. Draw a right triangle whose hypotenuse is of length 4 cm and one side is of length 2.5 cm.
Solution 2:
Construction:
Step 1. Make a 2.5-cm-long line segment QR.
Step 2. Make a 90o ∠QRX.
Step 3. Make an arc of the triangle with a middle Q and a radius PQ = 4 cm to intersect ray RX at P.
Step 4. Combine PQ and PQR to form the ideal triangle PQR.
Step 5. The required triangle is PQR.
Question :3. Draw a right triangle having hypotenuse of length 5.4 cm, and one of the acute angles of measure 30o
Solution 3:
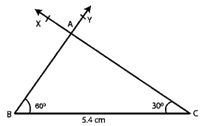
Let ABC be the right triangle at A such that hypotenuse BC = 5.4 cm. Let C = 30o.
Therefore ∠A + ∠B + ∠C = 180o
∠B = 180o − 30o− 90o = 60o
Construction:
Step 1. Make a BC = 5.4 cm line section.
Step 2. Make a 60o angle CBY.
Step 3. Make a 30o angle BCX on the same side of BC as Y, with X on the same side of BC as Y.
Step 4. Assume that BY and CX cross at A.
Step 5. The requisite triangle is then ABC.
Question :4. Construct a right triangle ABC in which AB = 5.8 cm, BC = 4.5 cm and ∠C = 90o.
Solution 4:
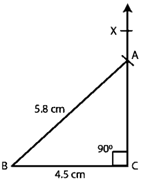
Construction:
Step 1. Make a BC = 4.5 cm line section.
Step 2. Make a BCX with a 90 o angle.
Step 3. Make an arc of the triangle to intersect ray CX at A, with center B and radius AB = 5.8 cm
Step 4. Connect AB to make the triangle ABC you want.
Step 5. The requisite triangle is ABC.
Question :5. Construct a right triangle, right angled at C in which AB = 5.2 cm and BC= 4.6 cm.
Solution 5:

Construction:
Step 1. Make a BC = 4.6 cm line section.
Step 2. Make ∠BCX of measure 90o
Step 3. Make an arc of the triangle with a center B and a radius AB = 5.2 cm that intersects ray CX at A.
Step 4. To get the desired triangle ABC, connect AB.
Step 5. The requisite triangle is ABC.

