Find BITSAT Mathematics Three Dimensional Geometry MCQs below. Practice the MCQ Questions for BITSAT Three Dimensional Geometry Mathematics with answers designed around official BITSAT, NCERT, and KVS styles. Look into more chapter-wise MCQs for BITSAT BITSAT Mathematics and grab additional latest study materials for all subjects.
Chapter MCQs: BITSAT Mathematics Three Dimensional Geometry
Are you studying BITSAT Mathematics? Look at these 50 questions with answers to make your core concepts of Three Dimensional Geometry very clear.
Three Dimensional Geometry Questions & Answers (BITSAT Mathematics)
Question: A line segment has length 63 and direction ratios are 3, –2, 6. If the line makes an obtuse angle with x–axis, the components of the line vector are
- a) 27, – 18, 54
- b) – 27, 18, 54
- c) – 27, 18, –54
- d) 27, – 18, – 54
Answer: – 27, 18, –54
Question: The line,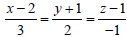
intersects the curve xy = c2, z = 0 if c is equal to
- a)
- b)
- c)
- d) None of these
Answer:
Question: The angle between two planes is equal to
- a) The angle between the tangents to them from any point
- b) The angle between the normals to them from any point
- c) The angle between the lines parallel to the planes from any point
- d) None of these
Answer: The angle between the normals to them from any point
Question: What is the angle between the lines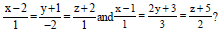 
- a)
- b)
- c)
- d) None of these
Answer:
Question: Find the direction cosines of the line joining the points A(6, –7, –1) and B (2, –3, 1).
- a)
- b)
- c)
- d)
Answer:
Question: Find the equation of the line 3x – 6y – 2z – 15 = 2x + y – 2z + 5= 0 in parametric form.
- a)
- b)
- c)
- d)
Answer:
Question: The point of intersection of the lines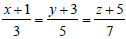
and
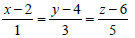is
- a)
- b)
- c)
- d) None of these
Answer:
Question: The equation of line of intersection of planes 4x + 4y – 5z = 12, 8x + 12y – 13z = 32 can be written as
- a)
- b)
- c)
- d)
Answer:
Question: The ratio in which the join of ( 2, 1, 5) and (3, 4, 3) is divided by the plane (x + y – z) =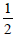
is
- a) 3 : 5
- b) 5 : 7
- c) 1 : 3
- d) 4 : 5
Answer: 5 : 7
Question: Two lines L1 : x 5,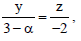
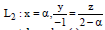are coplanar. Then, a can take value (s)
- a) 1, 4, 5
- b) 1, 2, 5
- c) 3, 4, 5
- d) 2, 4, 5
Answer: 1, 4, 5
Question: The ratio in which the join of ( 2, 1, 5) and (3, 4, 3) is divided by the plane (x + y – z) =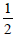 is
- a) 3 : 5
- b) 5 : 7
- c) 1 : 3
- d) 4 : 5
Answer: 5 : 7
Question: If the line through the points A (k, 1, –1) and B (2k, 0, 2) is perpendicular to the line through the points B and C (2 + 2k , k, 1), then what is the value of k?
- a) –1
- b) 1
- c) –3
- d) 3
Answer: 3
Question: Two lines L1 : x 5,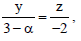 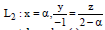are coplanar. Then, a can take value (s)
- a) 1, 4, 5
- b) 1, 2, 5
- c) 3, 4, 5
- d) 2, 4, 5
Answer: 1, 4, 5
Question: A line makes the same angle θ with each of the X and Z-axes. If the angle β, which it makes with Y-axis, is such that sin2 β = 3sin2 θ, then cos2 θequals
- a) 2/5
- b) 1/5
- c) 3/5
- d) 2/3
Answer: 3/5
Question: Find the angle between the line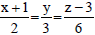
and the plane 10x + 2y – 11z = 3.
- a)
- b)
- c)
- d)
Answer:
Question: The equation of the right bisector plane of the segment joining (2, 3, 4) and (6, 7, 8) is
- a) x + y + z + 15 = 0
- b) x + y + z – 15 = 0
- c) x – y + z – 15 = 0
- d) None of these
Answer: x + y + z – 15 = 0
Question: The coordinates of the point where the line through the points A (3, 4, 1) and B (5, 1, 6) crosses the XY - plane are
- a)
- b)
- c)
- d)
Answer:
Question: Find the angle between the two planes 2x + y – 2z = 5 and 3x – 6y – 2z = 7
- a) cos–1 (4/21)
- b) cos–1 (2/21)
- c) cos–1 (1/21)
- d) cos–1 (5/21)
Answer: cos–1 (4/21)
Question: What is the value of n so that the angle between the lines having direction ratios (1, 1, 1) and (1, –1, n) is 60°?
- a) √3
- b) √6
- c) 3
- d) None of these
Answer: √6
Question: The foot of the perpendicular from the point (7, 14, 5) to the plane 2x + 4y – z = 2 are
- a) (1, 2, 8)
- b) (3, 2, 8)
- c) (5, 10, 6)
- d) (9, 18, 4)
Answer: (1, 2, 8)
Question: Find the coordinates of the point where the line joining the points (2, –3, 1) and (3, – 4, – 5) cuts the plane 2x + y + z = 7.
- a) (1, 2, – 7)
- b) (1, – 2, 7)
- c) (–1, – 2, 7)
- d) (1, 2, 7)
Answer: (1, – 2, 7)
Question: Gives the line L :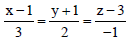
and the plane π : x – 2y – z = 0. Of the following assertions, the only one that is always true is
- a)
- b) L lies in π
- c) L is not parallel to π
- d) None of these
Answer: L lies in π
Question: The perpendicular distance of P(1, 2, 3) from the line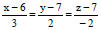
is
- a) 7
- b) 5
- c) 0
- d) 6
Answer: 7
Question: The equation of the plane containing the line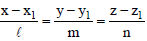
is a (x – x1) + b (y – y1) + c (z – z1) = 0. Correct option is
- a) ax1 + by1 + cz1 = 0
- b) al + bm + cn = 0
- c)
- d) lx1 + my1 + nz1 = 0
Answer: al + bm + cn = 0
Question: If the line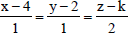 
lies in the plane 2x – 4y + z = 7, then the value of k is
- a) 4
- b) -7
- c) 7
- d) No real value
Answer: 7
Free study material for Mathematics
Practice MCQs for BITSAT Mathematics Three Dimensional Geometry
Practice MCQs: Three Dimensional Geometry (BITSAT)
Review these MCQs for Three Dimensional Geometry to check your active preparation status. Aligned with current BITSAT standards for BITSAT Mathematics, these multiple-choice sets offer targeted daily drills. Routine practice on these objective questions ensures a solid grasp of key concepts for upcoming tests.
NCERT-Aligned MCQs for BITSAT Mathematics
Compiled directly from the official NCERT book for BITSAT, these Mathematics MCQs focus on high-yield exam areas frequently tested in evaluations. Once finished, cross-reference your answers with our given solutions. To deepen your understanding of Three Dimensional Geometry, read through our professional NCERT solutions for BITSAT Mathematics.
Online Practice and Revision for Three Dimensional Geometry Mathematics
To gear up for examinations, try taking the free online BITSAT Mathematics MCQ test available on our platform. This tool is designed to enhance your response speed and accuracy. Consistent revision of these Mathematics topics builds absolute confidence across all core chapters.
FAQs
You can get most exhaustive BITSAT Mathematics Three Dimensional Geometry MCQs for free on StudiesToday.com. These MCQs for BITSAT Mathematics are updated for the 2026-27 academic session as per BITSAT examination standards.
Yes, our BITSAT Mathematics Three Dimensional Geometry MCQs include the latest type of questions, such as Assertion-Reasoning and Case-based MCQs. 50% of the BITSAT paper is now competency-based.
By solving our BITSAT Mathematics Three Dimensional Geometry MCQs, BITSAT students can improve their accuracy and speed which is important as objective questions provide a chance to secure 100% marks in the Mathematics.
Yes, Mathematics MCQs for BITSAT have answer key and brief explanations to help students understand logic behind the correct option as its important for 2026 competency-focused BITSAT exams.
Yes, you can also access online interactive tests for BITSAT Mathematics Three Dimensional Geometry MCQs on StudiesToday.com as they provide instant answers and score to help you track your progress in Mathematics.