BITSAT Mathematics Application Of Derivatives MCQs

Question: If f (x) = x^x, then f (x) is increasing in interval :

• a) [0, e]
• b)

  

• c) [0, 1]
• d) None of these

Answer:

Question: A cylindircal gas container is closed at the top and open at the bottom. if the iron plate of the top is 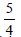time as thick as the plate forming the cylindrical sides. The ratio of the radius to the height of the cylinder using minimum material for the same capacity i

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: The set of all values of a for which the function f(x) = (a² – 3a + 2) (cos²x/4 –sin²x/4) + (a –1) x + sin 1does not possess critical points is

• a) [1, ∞)
• b)

  

• c)  (–2, 4) 
• d)

  

Answer:

Question: Match List I with List II and select the correct answer using the code given below the lists:

• a) (A) (B) (C) (D)

       1     4    5   3

• b) (A) (B) (C) (D)

       1    3    5   4

• c)   (A) (B) (C) (D)

         5   4    2    3

• d) (A) (B) (C) (D)

       5    3    2   4

Answer:  (A) (B) (C) (D)

                 5   4    2    3

Question:  What is the x-coordinate of the point on the curve 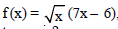where the tangent is parallel to x-axis?

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: A wire 34 cm long is to be bent in the form of a quadrilateral of which each angle is 90°. What is the maximum area which can be enclosed inside the quadrilateral?

• a) 68 cm² 
• b) 70 cm²
• c) 71.25 cm²
• d) 72. 25 cm²

Answer: 72. 25 cm²

Question: Consider the following statements in respect of the function

f (x) = x³ – 1, xÎ[-1,1]

I. f (x) is increasing in [– 1, 1]

II. f (x) has no root in (– 1, 1).

Which of the statements given above is/are correct?

• a) Only I
• b) Only II
• c) Both I and II
• d) Neither I nor II

Answer: Only I

Question: At an extreme point of a function f (x), the tangent to the curve is

• a) Parallel to the x-axis
• b) Perpendicular to the x-axis
• c) Inclined at an angle 45° to the x-axis
• d) Inclined at an angle 60° to the x-axis

Answer: Parallel to the x-axis

Question: The curve y = xe^x has minimum value equal to

• a)

  

• b)

  

• c)

  – e

• d) e

Answer:

Question: The line which is parallel to X-axis and crosses the curve y = √x at an angle of 45°, is

• a)

  

• b)

  

• c)

  

• d) y = 1

Answer:

Question: Tangents are drawn from the origin to the curve y = cos x. Their points of contact lie on

• a) x²y² = y² – x²
• b) x²y² = x² + y²
• c) x²y² = x² – y²
• d) None of these

Answer: x²y² = x² – y²

Question: The slope of the tangent to the curve y = e^x cos x is minimum at x = α,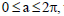, then the value of a is

• a) 0
• b) π
• c) 2π
• d) 3π/2

Answer: π

Question: The function 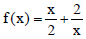has a local minimum at

• a) x = 2
• b) x = –2
• c) x = 0
• d) x = 1

Answer: x = 1

Question: If a and b are non-zero roots of x² + ax + b = 0 then the least value of x² + ax + b is

• a)

  

• b)

  

• c)

  

• d) 1

Answer:

Question: If 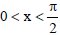 , then

• a) tan x < x < sin x
• b) x < sin x < tan x
• c) sin x < tan x < x
• d) None of these

Answer: None of these

Question: The interval in which the function 2x³ + 15 increases less rapidly than the function 9x² – 12x, is –

• a) (–∞, 1)
• b) (1, 2)
• c) (2, ∞)
• d) None of these

Answer: (1, 2)

Question: The fuel charges for running a train are proportional to the square of the speed generated in miles per hour and costs  48 per hour at 16 miles per hour. The most economical speed if the fixed charges i.e. salaries etc. amount to `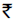300 per hour is

• a) 10
• b) 20
• c) 30
• d) 40

Answer: 40 

Question: The equation of all lines having slope 2 which are tangent to the curve 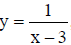 x≠3 is

• a) y = 2
• b) y = 2x
• c) y = 2x + 3
• d) None of these

Answer: None of these

Question: The function f (x) = (x(x–2))² is increasing in the set

• a)

  

• b) (– ∞, 1)
• c)

  

• d) (1, 2)

Answer:

Question: If a² x⁴ + b² y⁴ = c⁴, then the maximum value of xy is

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: If 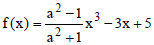is a decreasing function of x in R then the set of possible values of a (independent of x) is

• a) (1, ∞)
• b) (-∞, -1)
• c) [-1, 1]
• d) None of these

Answer: [-1, 1]

Question: The diagonal of a square is changing at the rate of 0.5 cm/sec. Then the rate of change of area, when the area is 400 cm², is equal to

• a)

  

• b) 10 √2 cm² / sec
• c)

  

• d)

  

Answer: 10 √2 cm² / sec

Question: If the normal to the curve y = f (x) at the point (3,4) makes an angle 3p/4 with the positive x-axis, then f ' (3) =

• a) –1
• b) – 3/4
• c) 4/3
• d) 1

Answer: 1

Question: The function f(x) = sin x – kx – c, where k and c are constants, decreases always when

• a) k > 1
• b)

  

• c) k < 1
• d)

  

Answer:

Question: The minimum value of f (x) = sin⁴ x + cos⁴ x in the interval 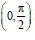 is

• a)

  

• b) 2
• c) √2
• d) 1

Answer:

Question: The curve y –e^xy+ x = 0 has a vertical tangent at

• a) (1, 1)
• b) (0, 1)
• c) (1, 0)
• d) No point

Answer: (1, 0)

Question: The function f(x) = 2x³ – 3x² – 12x + 4, has

• a) Two points of local maximum
• b) Two points of local minimum
• c) One maxima and one minima
• d) No maxima or minima

Answer: One maxima and one minima

Question: If a circular plate is heated uniformly, its area expands 3c times as fast as its radius, then the value of c when the radius is 6 units, is

• a) 4 π
• b) 2 π
• c) 6 π
• d) 3 π

Answer: 4 π

Question: The function f(x) = tan x – 4x is strictly decreasing on

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: The slope of the tangent to the hyperbola 2x² – 3y² = 6 at (3, 2) is

• a) –1
• b) 1
• c) 0
• d) 2

Answer: 1

Question: The minimum value of the function y = x⁴ – 2x² + 1 in the interval is

• a) 0
• b) 2
• c) 8
• d) 9

Answer: 0

Question: The value of a in order that f (x) = sin x – cos x – ax + b decreases for all real values is given by

• a)

  

• b) a < √2
• c)

  

• d) a < 1

Answer:

Question: The equation of tangent to the curve y = sin x at the point (π, 0) is

• a) x + y = 0
• b) x + y = π
• c) x – y =π
• d) x – y = 0

Answer: x + y = π

Question: If f(x) = cos x, then

• a) f(x) is strictly decreasing in (0, π)
• b) f(x) is strictly increasing in (0, 2π)
• c) f(x) is neither increasing nor decreasing in (π, 2π)
• d) All the above are correct

Answer:  f(x) is strictly decreasing in (0, π)

Question: The greatest value of f (x) = cos (xe^[x] + 7x² – 3x),x £ [–1, ∞) is –

• a) –1
• b) 1
• c) 0
• d) None of these

Answer: 1

Question: The function f (x) = cot^–1 x + x increases in the interval

• a) (1,∞)
• b) (–1,∞)
• c) (–∞, ∞)
• d) (0, ∞)

Answer: (–∞, ∞)

Question: The total revenue in rupees received from the sale of x units of a product is given by R(x) = 13x² + 26x + 15. Then the marginal revenue in rupees, when x = 15 is

• a) 116
• b) 126
• c) 136
• d) 416

Answer: 416

Question: If at any point S of the curve by² = (x + a)³, the relation between subnormal SN and subtangent ST be p (SN) = q (ST)² then p/q is equal to

• a) 8b/27
• b) 8a/27
• c) b/a
• d) None of these

Answer: 8b/27

Question: The equation of one of the tangents to the curve y = cos(x +y), 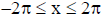 that is parallel to the line x + 2y = 0, is

• a) x + 2y = 1
• b) x + 2y = π/2
• c) x + 2y = π/4
• d) None of these

Answer: x + 2y = π/2

Question: For all values of x, function f (x) = 2x³ + 6x² + 7x – 19 is

• a) Monotonic increasing
• b) Monotonic decreasing
• c) Not monotonic
• d) None of these

Answer: Monotonic increasing

Question:

 is

• a) increasing in [0,∞)
• b) Decreasing in [0, ∞)
• c) 

  

• d)

  

Answer: Decreasing in [0, ∞)

Question: The largest value of y = 2x³ – 3x² – 12x + 5 for  occurs at x is equal to :

• a) -2
• b) -1
• c) 2
• d) 4

Answer: -1

Question: Function f(x) = cos x – 2λx is monotonic decreasing when

• a) λ > 1/2
• b) λ < 1/2
• c) λ < 2
• d) λ > 2

Answer: λ > 1/2

Question: The curve y –e^xy+ x = 0 has a vertical tangent at

• a) (1, 1)
• b) (0, 1)
• c) (1, 0)
• d) No point

Answer: (1, 0)

Question: The slope of the tangent to the hyperbola 2x² – 3y² = 6 at (3, 2) is

• a) -1
• b) 1
• c) 0
• d) 2

Answer: 1