BITSAT Mathematics Sequences and Series MCQs

Question: If A, B, C are the angles of a triangle and e^iA,e^iB,e^iC are in A.P. Then the triangle must be

• a) Right angled
• b) Isosceles
• c) Equilateral
• d) None of these

Answer: Equilateral

Question: If

 where p, q, t and s are constants, then the value of s is equal to

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: After striking the floor a certain ball rebounds 4/5th of its height from which it has fallen. The total distance that the ball travels before coming to rest if it is gently released from a height of 120m is

• a) 960 m
• b) 1000 m
• c) 1080 m
• d) Infinite

Answer: 1080 m

Question: 2^1/4. 2^2/8. 2^3/16. 2^4/32......∞ is equal to-

• a) 1
• b) 2
• c) 3/2
• d) 5/2

Answer: 2

Question: The fourth term of an A.P. is three times of the first term and the seventh term exceeds the twice of the third term by one, then the common difference of the progression is

• a) 2
• b) 3
• c)

  

• d) -1

Answer: 2

Question: The sum to n terms of the series 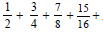 __________ is

• a) n – 1 – 2^{– n}
• b) 1
• c) n – 1 + 2^{– n}
• d) 1 + 2^{– n}

Answer: n – 1 + 2^{– n}

Question: If log a, log b, and log c are in A.P. and also log a– log 2b, log 2b – log 3c, log 3c – log a are in A.P., then

• a) a, b, c, are in H.P
• b) a, 2b, 3c are in A.P.
• c) a, b, c are the sides of a triangle
• d) None of these

Answer: a, b, c are the sides of a triangle

Question:

upto n terms is

• a)

  

• b)

  

• c)

  

• d) None of these

Answer:

Question: If ω is the complex cube root of unity, then the value of ω+ ω 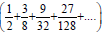 is

• a) -1
• b) 1
• c) -i
• d) i

Answer: -1

Question: The value of .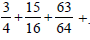

____ upto n terms is

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: If binomial coefficients of three consecutive terms of (1 + x)ⁿ are in HP, then the maximum value of n is

• a) 1
• b) 2
• c) 0
• d) None of these

Answer: None of these

Question: If the (2p)^th term of a H.P. is q and the (2q)^th term is p, then the 2(p + q)^th term is-

• a) 

  

• b)

  

• c)

  

• d)

  

Answer:

Question: If 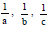  are A. P., then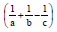 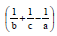  is equal to

• a)

  

• b)

  

• c)

  

• d) None of these

Answer:

Question: The product of n positive numbers is unity, then their sum is :

• a) A positive integer
• b) Divisible by n
• c)

  

• d) Never less than n

Answer:  Never less than n

Question: Let T_r be the r^th term of an A.P. for r = 1, 2, 3, .... If for some positive integers m, n we have 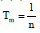 and 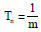  then T_mn equals

• a)

  

• b)

  

• c) 1
• d) 0

Answer: 1

Question: If x is positive then the sum to infinity of the series 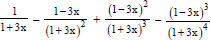 ........... ∞ is

• a) 1/2
• b)

  

• c)

  

• d)

  

Answer: 1/2

Question: If p^th,q^th and r^th terms of H.P. are u,v,w respectively, then find the value of the expression (q – r) vw + (r – p) wu + (p – q) uv.

• a) 2
• b) 0
• c) 4
• d) 8

Answer: 0

Question: If the sum of the first 2n terms of 2, 5, 8, ....... is equal to the sum of the first n terms of 57, 59, 61......., then n is equal to

• a) 10
• b) 12
• c) 11
• d) 13

Answer: 11

Question: If m arithmetic means are inserted between 1 and 31 so that the ratio of the 7^th and (m – 1)^th means is 5 : 9, then find the value of m

• a) 14
• b) 24
• c) 10
• d) 20

Answer: 14

Question: The 100^th term of the sequence 1, 2, 2, 3, 3, 3, 4, 4, 4, 4,... is

• a) 12
• b) 13
• c) 14
• d) 15

Answer: 14

Question: The n^th term of a GP is 128 and the sum of its n terms is 255. If its common ratio is 2 then find the first term.

• a) 1
• b) 2
• c) 3
• d) 4

Answer: 1

Question: Find the geometric mean of numbers 7, 7², 7³,.......,7ⁿ

• a)

  

• b)

  

• c)

  

• d)

  

Answer:

Question: Sum to 20 terms of the series 1.3² + 2.5² + 3.7² +... is

• a) 178090
• b) 168090
• c) 188090
• d) 190090

Answer: 188090

Question: The sum of infinite terms of the geometric progression ............is

• a) √2( √2 +1)²
• b) ( √2 +1)²
• c) 5 √2
• d) 3 √2 + √5

Answer: √2( √2 +1)²

Question: If the non-zero numbers x, y, z are in A. P. and tan ^–1x, tan ^–1y, tan ^–1 z are in A. P. then

• a) x = y = z
• b) y = zx
• c) x = yz
• d) z = xy

Answer: x = y = z

Question: 8^th term of the series 2 √2, √2,0,..... will be –

• a) -5 √2
• b) 5 √2
• c) 10 √2
• d) -10 √2

Answer: -5 √2

Question: a, b, c are first three terms of a G.P. If HM of a and b is 12 and that of b and c is 36, then find the value of a.

• a) 6
• b) 12
• c) 10
• d) 8

Answer: 8

Question: If the sum of the first 2n terms of 2, 5, 8, ....... is equal to the sum of the first n terms of 57, 59, 61......., then n is equal to

• a) 10
• b) 12
• c) 11
• d) 13

Answer: 11

Question: If m arithmetic means are inserted between 1 and 31 so that the ratio of the 7^th and (m – 1)^th means is 5 : 9, then find the value of m.

• a) 14
• b) 24
• c) 10
• d) 20

Answer: 14

Question: The 100^th term of the sequence 1, 2, 2, 3, 3, 3, 4,4, 4, 4,... is

• a) 12
• b) 13
• c) 14
• d) 15

Answer: 14